Expectation Values
To relate a quantum mechanical calculation to something you can observe in the laboratory, the "expectation value" of the measurable parameter is calculated. For the position x, the expectation value is defined as
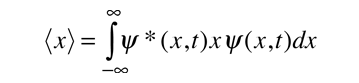
This integral can be interpreted as the average value of x that we would expect to obtain from a large number of measurements. Alternatively it could be viewed as the average value of position for a large number of particles which are described by the same wavefunction. For example, the expectation value of the radius of the electron in the ground state of the hydrogen atom is the average value you expect to obtain from making the measurement for a large number of hydrogen atoms.
While the expectation value of a function of position has the appearance of an average of the function, the expectation value of momentum involves the representation of momentum as a quantum mechanical operator.
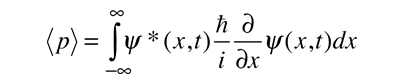
where
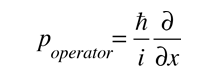
is the operator for the x component of momentum.
Since the energy of a free particle is given by

and the expectation value for energy becomes
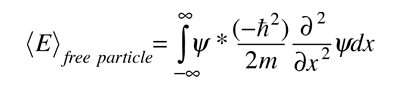
for a particle in one dimension.
In general, the expectation value for any observable quantity is found by putting the quantum mechanical operator for that observable in the integral of the wavefunction over space:
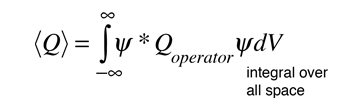
Schrodinger equation concepts
Postulates of quantum mechanics
| HyperPhysics***** Quantum Physics | R Nave |