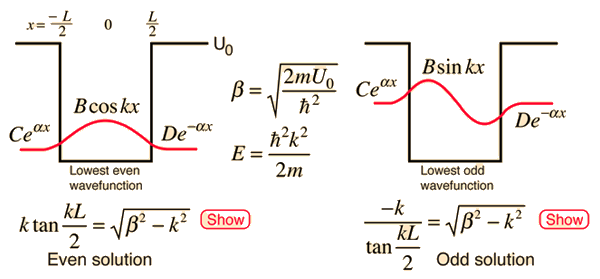
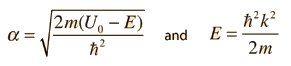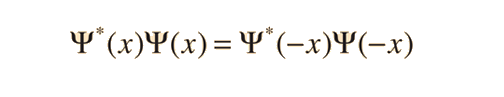Particle in Finite-Walled Box

Given a potential well as shown and a particle of energy less than the height of the well, the solutions may be of either odd or even parity with respect to the center of the well. The Schrodinger equation gives trancendental forms for both, so that numerical solution methods must be used.

Even Solution, Finite Box

This last step makes use of the substitution that was used in the setup of the finite well problem:

The standard constraints on the wavefunction require that both the wavefunction and its derivative be continuous at any boundary. Applying such constraints is often the way that the solution is forced to fit the physical situation.

Numerical Solution for Ground State

The ground state solution for a finite potential well is the lowest even parity state and can be expressed in the form where . Since both sides of the equation are dependent on the energy E for which you are solving, the equation is trancendental and must be solved numerically. One way to estimate the ground state energy of a finite potential well is to use the infinite well energy to produce a trial attenuation factor α. Then the value of α can be refined by iteration to get an effective well width and a numerical solution for the energy.

Odd Solution, Finite Box

This last step makes use of the substitution that was used in the setup of the finite well problem:

The standard constraints on the wavefunction require that both the wavefunction and its derivative be continuous at any boundary. Applying such constraints is often the way that the solution is forced to fit the physical situation.

Parity and the Particle in a Box

In the one-dimensional case, parity refers to the "evenness" or "oddness" of a function with respect to reflection about x=0.

The particle in a box problem can give some insight into the importance of parity in quantum mechanics. The box has a line of symmetry down the center of the box (x=0). Basic considerations of symmetry demand that the probability for finding the particle at -x be the same as that at x. The condition on the probability is given by:

This condition is satisfied if the parity is even or odd, but not if the wavefuntion is a linear combination of even and odd functions. This can be generalized to the statement that wavefunctions must have a definite parity with respect to symmetry operations in the physical problem.