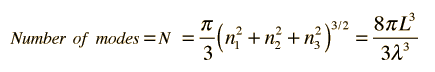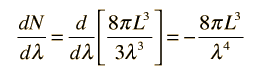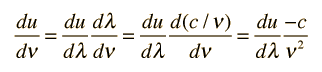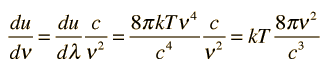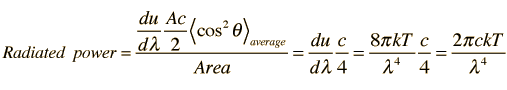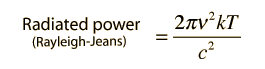Electromagnetic Waves in a Cubical Cavity
Electromagnetic standing waves in a cavity at equilibrium with its surroundings cannot take just any path. They must satisfy the wave equation in three dimensions:
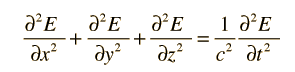
The solution to the wave equation must give zero amplitude at the walls, since a non-zero value would dissipate energy and violate our supposition of equilibrium. To form a standing wave, the reflection path around the cavity must produce a closed path. The boundary conditions can be met with a solution of the form:

Substituting this solution into the wave equation above gives

which simplifies to

How many modes of this wavelength? | Development of the Rayleigh-Jeans Law |
Rayleigh- Jeans references
Blackbody radiation concepts
| HyperPhysics***** Quantum Physics | R Nave |
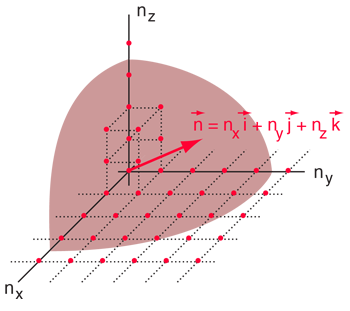
 .
.