Taylor Series

If f(x) is a well-behaved* function near a chosen expansion point, x₀, then the function can be expanded in a series called a Taylor series:

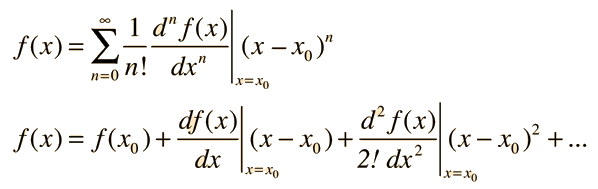
The Taylor series for a function is often useful in physical situations to approximate the value of the function near the expansion point x₀. It may be evaluated term-by-term in terms of the derivatives of the function. It is typical for successive terms in a series approximation of a function to get smaller and smaller, and when the size of the next term appears negligible in terms of the problem being addressed, then one can judge that a sufficiently accurate approximation of the function has been achieved.

It is often the case that a convenient expansion point is x₀ = 0, and series about this special expansion point are also called Maclaurin series. There are many applications for expansions of common functions around x=0. Some examples are:

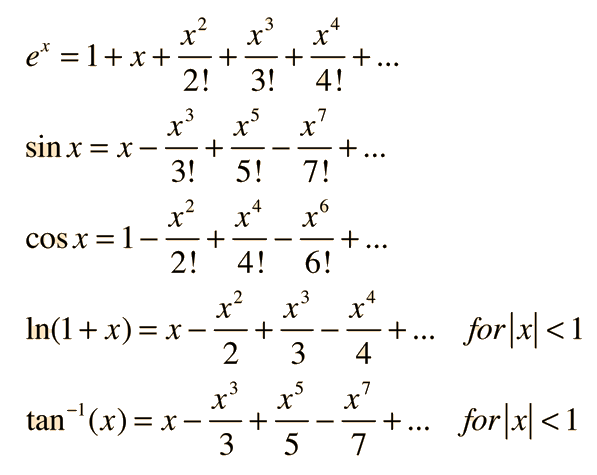
The one-term approximation for trig function series have many applications as "small angle approximations".

* Well-behaved means that both the function and its derivatives are defined and continuous in the range of the expansion around x₀.