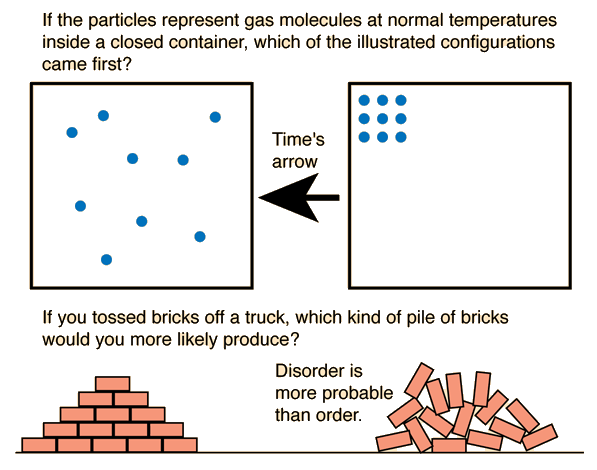
Entropy as Time's Arrow
One of the ideas involved in the concept of entropy is that nature tends from order to disorder in isolated systems. This tells us that the right hand box of molecules happened before the left.
|
Using Newton's laws to describe the motion of the molecules would not tell you which came first. For an isolated system, entropy always increases or remains the same, so if you compare states of different entropy, the one with the greater entropy will be later in time.
|
Caveats and Objections
There are some subtleties in the nature of entropy and other thermodynamic quantities, subtleties that we try to put into word pictures and sketches which sometimes oversimplify. In teaching thermodynamics, I have always tried to keep in mind the words of one of the great physics teachers of the mid-20th century, Mark Zemansky:
is as easy as a song:
You think you make it simpler
when you make it slightly wrong."
The diagrams above have generated a lively discussion, partly because of the use of order vs disorder in the conceptual introduction of entropy. It is typical for physicists to use this kind of introduction because it quickly introduces the concept of multiplicity in a visual, physical way with analogies in our common experience. Chemists, on the other hand, often protest this approach because in chemical applications order vs disorder doesn't communicate the needed ideas on the molecular level and can indeed be misleading. The very fact of differences of opinion on the use of order and disorder can itself be instructive.
The top diagram depicts time's arrow as pointing from order to disorder, but one must admit that the apparent tendency to move from order to disorder is not the most fundamental way to look at the top diagram. At ordinary temperatures, the internal energy of a gas would give the molecules high velocities, and it is evident that this orderly arrangement would be very rare because there are only a few ways to do it. If it occurred, it would be for a brief instant and then the molecules would move to some other configuration. The diagram at left depicts a more random or disordered configuration, but the key point is that there is a vast number of ways that such configurations could be achieved. So multiplicity is the key concept - molecular ensembles will spontaneously tend to evolve from configurations of lower multiplicity to configurations of greater multiplicity.
The bottom diagram is again a picture with which common experience immediately identifies - there are more ways to create a jumbled pile of bricks than a neatly stacked arrangement. Again, the idea of multiplicity is the key point. Objections to this kind of introduction to entropy come from the fact that the useful applications of entropy are thermodynamic ones and involve nature on the atomic and molecular scale. The ordered bricks vs the jumbled pile may be a useful introductory visualization, but if these two piles of bricks were at the same temperature, then the numerical value of the entropy would be almost identical for the two stacks. If the contributions to entropy involves the multiplicity of the ways that the vast number of molecules in the two stacks of bricks can be arranged, then the fact that the macroscopic orientations of the bricks is different is a negligible contribution to the total entropy. Entropy is a crucial microscopic concept for describing the thermodynamics of systems of molecules, and the assignment of entropy to macroscopic objects like bricks is of no apparent practical value except as an introductory visualization.
Entropy concepts
| HyperPhysics***** Thermodynamics | R Nave |
Entropy and DisorderIf you assert that nature tends to take things from order to disorder and give an example or two, then you will get almost universal recognition and assent. It is a part of our common experience. Spend hours cleaning your desk, your basement, your attic, and it seems to spontaneously revert back to disorder and chaos before your eyes. So if you say that entropy is a measure of disorder, and that nature tends toward maximum entropy for any isolated system, then you do have some insight into the ideas of the second law of thermodynamics. Some care must be taken about how you define "disorder" if you are going to use it to understand entropy. A more precise way to characterize entropy is to say that it is a measure of the "multiplicity" associated with the state of the objects. If a given state can be accomplished in many more ways, then it is more probable than one which can be accomplished in only a few ways. When "throwing dice", throwing a seven is more probable than a two because you can produce seven in six different ways and there is only one way to produce a two. So seven has a higher multiplicity than a two, and this gives some insight why systems in nature like the molecules of a gas would spontaneously tend toward states of higher multiplicity or higher "entropy".
| Index Entropy concepts | |||
|
Go Back |