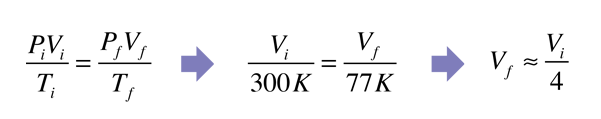Ideal Gas Law and the Shrinking balloon in liquid nitrogen

| |

| Applying the ideal gas law to the gas above the liquid nitrogen in a vacuum flask suggests that the volume of a balloon placed in it would reduce to one-fourth its volume. Actually, it reduces much more than that - virtually removing all the gas in the balloon.
|
The expectation from the ideal gas law is summarized by
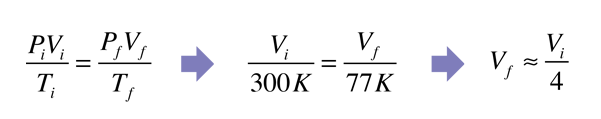
One step toward explaining the reduction in volume is the fact that all the moisture in the air freezes out. But the moisture, even in saturated air at body temperature (from blowing up the balloon) provides a vapor pressure of only 47 mmHg, a reduction in volume of only about 6% of the total. The next suggestion is that the oxygen in the air will condense out. The boiling point of oxygen is 90K compared to the 77K for nitrogen, so would be expected to condense out. But the oxygen content of air is only 21% or about 159 mmHg, so that is not enough to explain the almost complete collapse.
So it is clear that most of the nitrogen itself from the air in the balloon liquifies to get the degree of collapse which is observed. The answer to why it condenses is not so clearcut. The air in the balloon is at an elevated pressure, and increasing the pressure will raise the boiling point temperature at which the gas can liquify, but that would appear to be a small effect. It seems that the main explanation comes from the fact that the air is a mixture and that the liquification of air occurs at a higher temperature than pure nitrogen gas, around 79 K at atmospheric pressure.
There are still some mysteries in the behavior of the balloon in liquid nitrogen. Since
Pascal's law dictates that the pressure is the same at all points inside the balloon,
then we know that when we put one end in the liquid nitrogen and it
starts to shrink while the end in our hand still appears normal, then the internal
pressure at that point has not changed significantly. Laplace's law gives us a
relationship between the balloon radius and the internal pressure, so as long
as a piece of the balloon is in the air and is close to its original radius, then we are
maintaining about the same internal pressure in the balloon. From the amount of the
balloon that we can get to collapse, we know that we have frozen out
the water content and liquified the oxygen and then have begun to liquify the nitrogen
inside the balloon. At this point there are still some uncertainties in my mind - the
inflation of a portion of the balloon still implies an internal
pressure above atmospheric, but I don't know how much pressure is required.
The balloon material remains remarkably airtight during this extreme process, as
indicated by the fact that you can cool and warm it up several times with no apparent
change in volume.
|
Index
Temperature concepts
Liquid nitrogen |