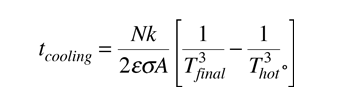Radiative Cooling Time

The rate of radiative energy emission from a hot surface is given by the Stefan-Boltzmann law .

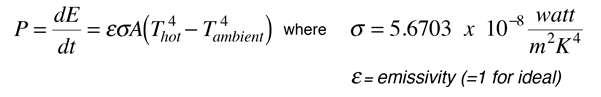
Here P is the power emitted from the area, and E is the energy contained by the object. For very hot objects, the role of the ambient temperature can be neglected. If the hot temperature is more than 3.16 times the ambient, then the contribution of ambient terms is less than 1%. For example, for 300K ambient on the earth, an object of temperature higher than 1000K can be treated like a pure radiator into space. If the heat loss is purely radiative and not limited by heat transfer to the radiating surface, then the cooling time can be modeled for a hot object.

If the energy of the object can be characterized by pure translational kinetic energy according to equipartition of energy, then

Using the chain rule for differentiation

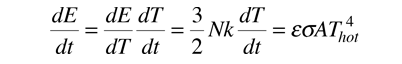
Rearranging gives us

and integrating gives the cooling time

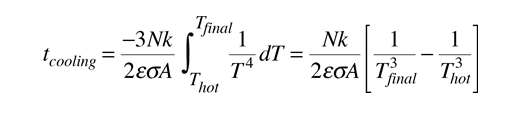
It must be kept in mind that for macroscopic objects, the calculated cooling time for the object as a whole will always be shorter than the real cooling time, so that it gives a lower bound. The above relationship assumes infinite thermal conductivity so that the temperature of the whole object is equal to the surface temperature. In the real world, the surface will cool faster than the interior. The rate of heat transfer from the interior will be expected to limit the rate of radiative loss from the surface.

Modeling the Radiative Cooling of a Hot Sphere

The modeling of the radiative cooling time of a hot sphere can give some insights into the role of radiation in cooling hot objects. Radiation is definitely not the only mechanism involved; the cooling of real macroscopic objects is a multifaceted topic including heat transfer from the interior of the object to the surface. With this caution about the applicability of these results to the real world, a model for the radiative cooling of a sphere will be developed. The model of the cooling time is given by

For a sphere of radius r = cm = m = x 10^m,

the surface area is A = cm² = x 10^ m².

the volume is V = cm³ = x 10^ m³.

If the density is gm/cm³ = kg/m³, then

the mass will be gm = kg = x10^ kg.

If the molar mass is known to be M = gm, then we can determine the number of atoms or molecules contained in the sphere. (Caution! These are assumed to be experimental numbers. Molar mass and density are not independent, and it is easy to choose values which are incompatible. Neither is the density precisely determined by the molar mass because of different crystal structures, etc. ). With these assumptions, the number of particles is modeled to be

= x10^

If the original high temperature is = K

then a cooling time of sec = x10^ sec

for an object with emissivity

corresponds to a final temperature K

In this calculation, the value of any parameter may be changed, and the default calculation will be the final temperature. However, if the final temperature is changed, the corresponding cooling time will be calculated.

While perhaps instructive as an exploration, this calculation is unrealistic because of several simplifying assumptions:

• The entire mass is presumed to be at the same temperature, whereas in any real object the surface will cool faster and you will have a lag in the transfer of heat from the interior of the object to the surface to be radiated.
• The effect of the ambient temperature is neglected. This may be justified. If the hot temperature is more than about three times the ambient, then the error from this assumption is down to 1%
• Other heat transfer processes are neglected, namely conduction and convection. For temperatures over 1000K, this is probably justified. Conduction and convection depend linearly upon temperature, while radiation goes up according to the fourth power.
• The derivative of energy with respect to temperature above is highly simplified. This derivative is really the specific heat of the object, and it is more involved than this simple expression.