Pressure and the Thermodynamic Identity
The thermodynamic identity can be used to obtain a relationship between pressure and entropy. If the internal energy is held constant, then the pressure can be expressed as
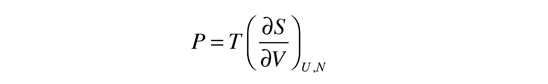
This definition implies that you are holding both the internal energy and the number of particles constant in taking the derivative. This can be applied to the expression for the entropy of a monoatomic ideal gas:

In order to take the partial derivative of this with respect to V to get the pressure, we use the rules for the logarithms of products to express the logarithm as just ln(V) plus some other log terms which do not contain V. All these other terms will drop out when the derivative is taken. Remember that the derivative of ln(V) is just 1/V. This gives us:
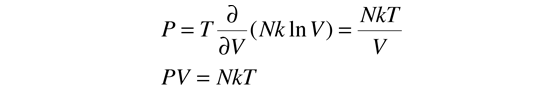
This relationship is just the ideal gas law! But the ideal gas law can be obtained from just Newton's laws, which give an expression for average pressure of a gas. That along with the kinetic temperature gives the form of the gas law. So, looking at it from the other direction, the ideal gas law offers confirmation of the relationship between pressure and entropy.
Internal energy concepts
Entropy concepts
Reference
Schroeder
Ch 3
| HyperPhysics***** Thermodynamics | R Nave |