Motion concepts
| HyperPhysics***** Mechanics | R Nave |

|
Index Motion concepts | ||
|
Go Back |
|
Note that you can enter a distance (height) and click outside the box to calculate the freefall time and impact velocity in the absence of air friction. But the calculation assumes that the gravity acceleration is the surface value g = 9.8 m/s2, so if the height is great enough for gravity to have changed significantly the results will be incorrect.
|
Index Trajectory concepts | |||
|
Go Back |
| Index Trajectory concepts | |||
|
Go Back |

|
Index Trajectory concepts Calculation | ||
|
Go Back |
Horizontal Launch
| Index Trajectory concepts | ||
|
Go Back |
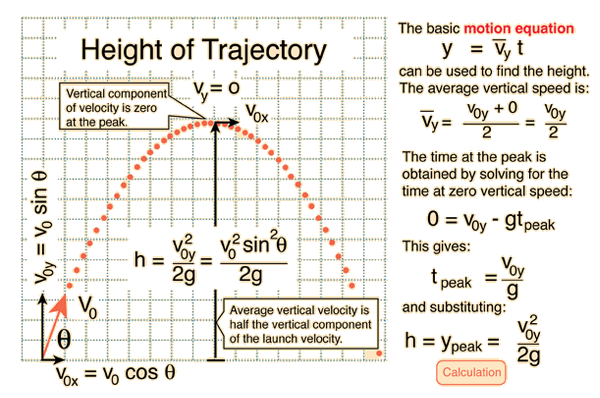
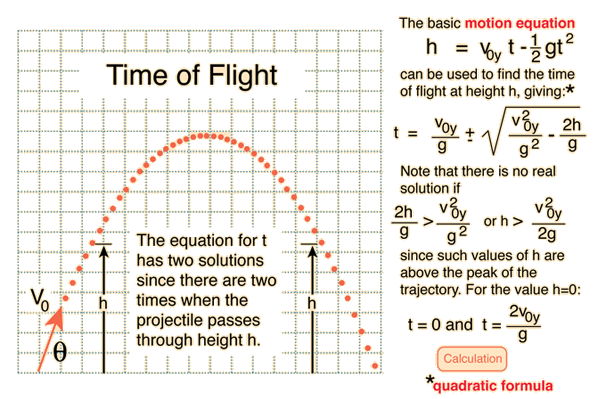
General Ballistic TrajectoryThe motion of an object under the influence of gravity is determined completely by the acceleration of gravity, its launch speed, and launch angle provided air friction is negligible. The horizontal and vertical motions may be separated and described by the general motion equations for constant acceleration. The initial vector components of the velocity are used in the equations. The diagram shows trajectories with the same launch speed but different launch angles. Note that the 60 and 30 degree trajectories have the same range, as do any pair of launches at complementary angles. The launch at 45 degrees gives the maximum range.
|
Index Trajectory concepts Calculation | ||
|
Go Back |
| Index Trajectory concepts | |||
|
Go Back |

|
Index Trajectory concepts | ||
|
Go Back |
|
Index Trajectory concepts | ||
|
Go Back |
|
Index Trajectory concepts | ||
|
Go Back |
| Index Trajectory concepts | |||
|
Go Back |
Will it clear the fence?The basic motion equations can be solved simultaneously to express y in terms of x. |
Index Trajectory concepts | ||
|
Go Back |
Where will it land?The basic motion equations give the position components x and y in terms of the time. Solving for the horizontal distance in terms of the height y is useful for calculating ranges in situations where the launch point is not at the same level as the landing point.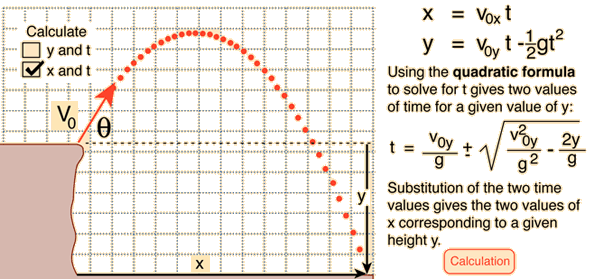
|
Index Trajectory concepts | ||
|
Go Back |
Where will it land?The basic motion equations give the position components x and y in terms of the time. Solving for the horizontal distance in terms of the height y is useful for calculating ranges in situations where the launch point is not at the same level as the landing point. |
Index Trajectory concepts | ||
|
Go Back |
Launch VelocityThe launch velocity of a projectile can be calculated from the range if the angle of launch is known. It can also be calculated if the maximum height and range are known, because the angle can be determined. |
Index Trajectory concepts | ||
|
Go Back |
Launch VelocityThe launch velocity of a projectile can be calculated from the range if the angle of launch is known. It can also be calculated if the maximum height and range are known, because the angle can be determined. |
Index Trajectory concepts | ||
|
Go Back |
Angle of LaunchVariation of the launch angle of a projectile will change the range. If the launch velocity is known, the required angle of launch for a desired range can be calculated from the motion equations. |
Index Trajectory concepts | ||
|
Go Back |

|
Index Trajectory concepts | ||
|
Go Back |