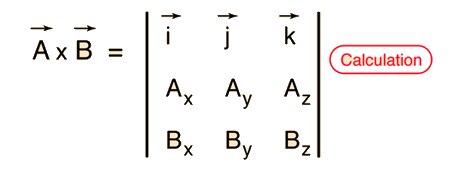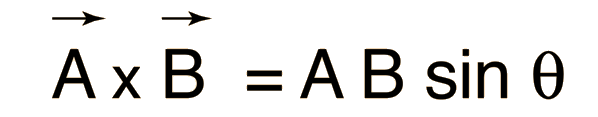Vector Product of Vectors
The vector product and the scalar product are the two ways of multiplying vectors which see the most application in physics and astronomy. The magnitude of the vector product of two vectors can be constructed by taking the product of the magnitudes of the vectors times the sine of the angle (<180 degrees) between them. The magnitude of the vector product can be expressed in the form:

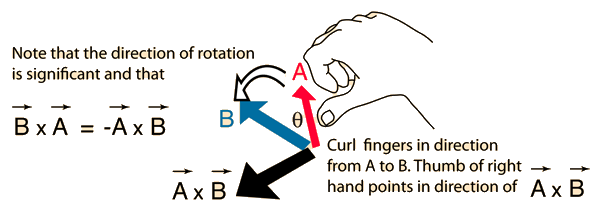
and the direction is given by the right-hand rule. If the vectors are expressed in terms of unit vectors i, j, and k in the x, y, and z directions, then the vector product can be expressed in the rather cumbersome form:

which may be stated somewhat more compactly in the form of a determinant.
Vector concepts
Applications
| HyperPhysics***** Mechanics | R Nave |