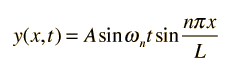Traveling Wave Parameters
A traveling wave solution to the wave equation may be written in several different ways with different choices of related parameters. These include the basic periodic motion parameters amplitude, period and frequency.
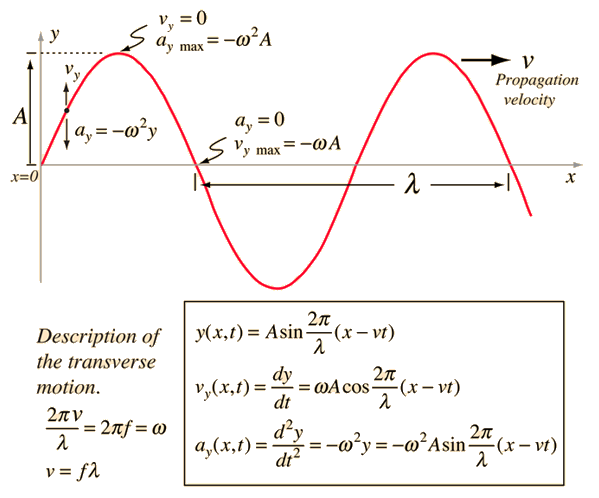
Equivalent forms of wave solution:

|
Wave parameters:
| *Amplitude A
*Period T = 1/f
*Frequency f = 1/T
*Propagation speed v
|
*Wavelength λ
*Wave number k = 2π/λ
*Angular frequency ω = 2πf
*Wave relationship v = fλ
|
|
The wave velocity is determined by the properties of the medium and is independent of the other parameters, but it can be determined from measurements of the frequency and wavelength. The following calculation allows you to specify any two of the quantities in the wave relationship v = fl and then initiate the calculation by clicking on the active text for the quantity you wish to calculate.

Note: The position, velocity and acceleration are recalulated only when you click on either velocity, frequency or wavelength in the active formula above.
|