Estimación de los Niveles de Sonidos con la Ley del Inverso del Cuadrado

En el mundo real, la ley del inverso del cuadrado es siempre una idealización, ya que supone que la propagación del sonido es exactamente igual en todas las direcciones. Si en el campo sonoro hay superficies reflectantes, entonces los sonidos reflejados se sumarán al sonido principal y se obtendrá más nivel de sonido en un lugar del campo del que predice la ley del inverso del cuadrado. Si hay obstáculos entre la fuente y el punto de medición, también se puede recibir menos que lo predicho por la ley del inverso del cuadrado. Sin embargo, la ley del inverso del cuadrado es la primera estimación lógica del sonido que se obtendría en un punto distante en una zona razonablemente abierta.

Si se mide un nivel de sonido de I1 = dB a una distancia d1 = m = pi entonces, a distancia d2 = m = ft la ley del inverso del cuadrado predice un nivel de sonido I2 = dB

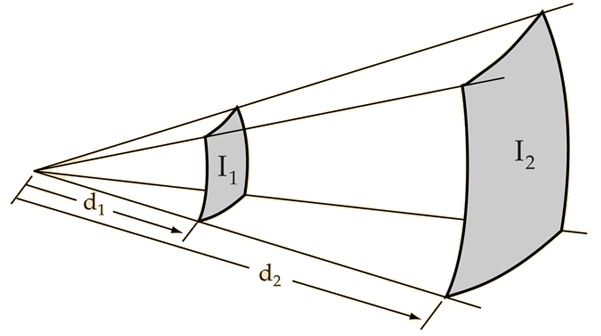
Se puede explorar numericamente para confirmar que doblando la distancia, la intensidad cae unos 6 dB y que a 10 veces la distancia, la intensidad cae unos 20 dB.