Work, Energy and Friction
Example of Energy Balance Calculations
In the "friction experiment" you collected data about distances and times for the masses involved. This data allows you to make calculations of the energies involved in the motions. One of the fundamental symmetries of nature is conservation of energy: "Energy is neither created nor destroyed.". This means that for any physical experiment, you should be able to "balance the energy checkbook" and account for the energies involved in different parts of the experiment. The experiment starts with an energy balance in the form of the gravitational potential energy of the mass hanging on the string. As the mass falls to the floor, you withdraw all of that balance, paying it out in the form of the kinetic energies of the falling mass and the moving block on the table above. The string attached to the block on the wooden runway does work on it which is force x distance. That work moves the block against the frictional resistance mmg where the weight is W=mg . It also gives it kinetic energy so that it is still moving for a time after the hanging mass hits the floor. Ultimately, friction wins out and stops the sliding block, and at that time you can say that all the work done on the block has been "withdrawn" from your energy account as it is dissipated against the frictional resistance. By balancing the energy checkbook, we can imply the work done against friction and determine a value for the coefficient of friction which acted between the block and the wooden track on which it is sliding.
The following is an example analysis from data taken in the laboratory. The detailed analysis has parallel input boxes where you may enter your data for comparison and determine the coefficient of friction from your own data. The data boxes will default to the values for the examples, so you will have to make sure that your values for the measurements are entered.
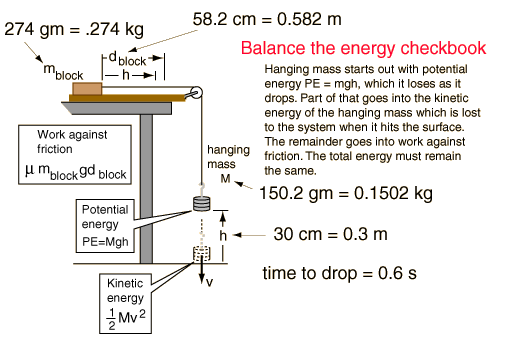
The first step in the analysis is to determine your initial energy balance, the potential energy of the hanging mass.
Apparatus movie