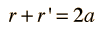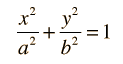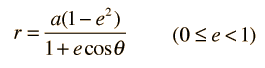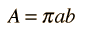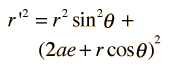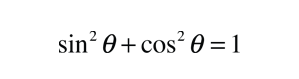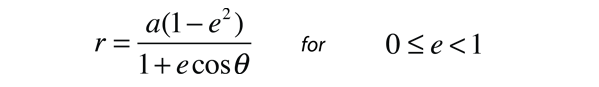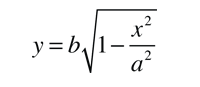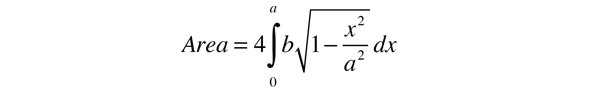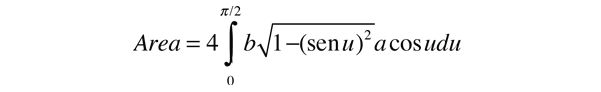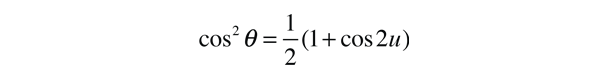Elipse y Órbitas Elípticas
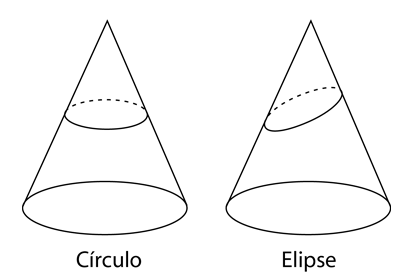 | La elipse se puede ver también como una sección cónica, la curva obtenida mediante el corte de un cono circular. Un corte perpendicular al eje nos da el caso especial del círculo. |
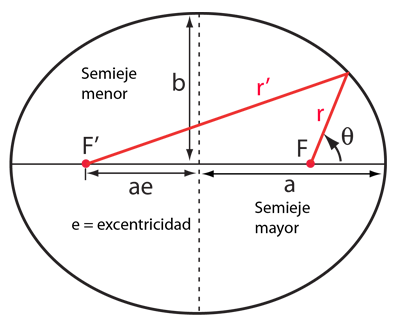
En la descripción de una órbita elíptica, es conveniente expresar la posición orbital, mediante coordenadas polares, usando el ángulo θ:
Esta es la forma conveniente para determinar el afelio y el perihelio de la órbita elíptica. El área de una elipse está dada por
Cada una de las secciones cónicas se puede describir en función del semieje mayor a y la excentricidad e. Se muestran los valores representativos de estos parámetros, junto con el tipo de órbita asociada con cada uno. | 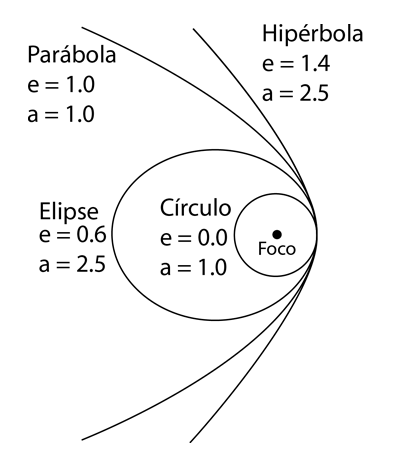 |
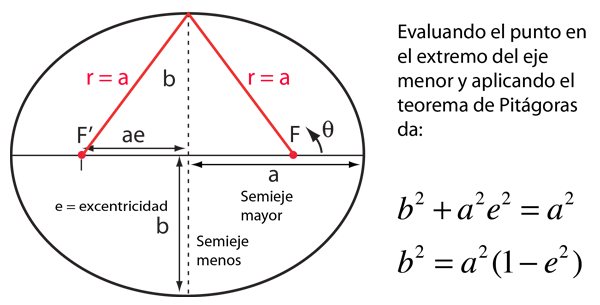
|
Índice |