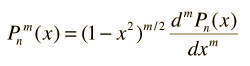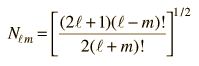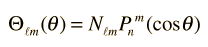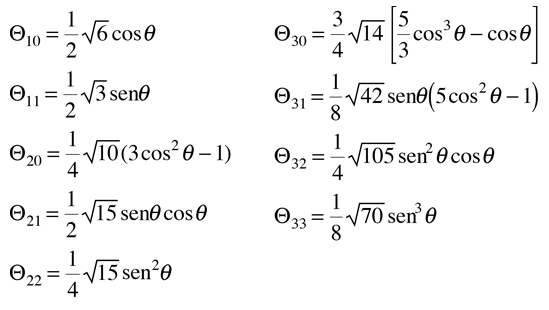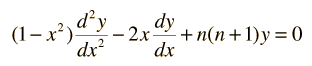
Polinomios de Legendre Una variedad de las funciones especiales que se encuentra en la solución de problemas físicos es la clase de funciones llamadas Polinomios de Legendre. Son la solución a una ecuación diferencial muy importante llamada ecuación de Legendre: Los polinomios se indican por medio de Pn(x) , llamados polinomio de Legendre de orden n. Los polinomios pueden ser tanto funciones par como impar de x, para ordenes de n par o impar. Abajo se muestran los primeros polinomios. 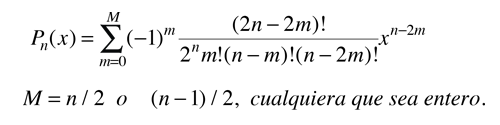La forma general de un polinomio de Legendre de orden n está dado por el sumatorio: De los polinomios de Legendre se pueden generar otra clase importante de funciones para los problemas físicos, las funciones de Legendre asociadas. La ecuación toma su nombre de Adrien Marie Legendre (1752-1833), un matemático francés que fué profesor en París en 1775. Realizó importantes contribuciones a las funciones especiales, integrales elípticas, teoría de números y el cálculo de variaciones. (Kreyszig).

Índice Referencia Kreyszig Sec 4.3

HyperPhysics*****HyperMath*****Cálculo M Olmo R Nave

Atrás

Funciones de Legendre Asociadas De los polinomios de Legendre se pueden derivar una clase importante de funciones especiales, llamadas funciones de Legendre asociadas. La fórmula que los define es donde Pn(x) es el polinomio de Legendre de orden n. Estas funciones son de gran importancia en la física cuántica, porque aparecen en las soluciones de la ecuación de Schrodinger en coordenadas polares esféricas. En ese contexto, la variable x se reemplaza por cosq, donde q es el ángulo que forma con la latitud. También en aquel contexto, las funciones de ondas que son soluciones a la ecuación de Schrodinger, necesitan ser normalizadas, de modo que la lista de funciones de abajo, incluirán el factor de normalización Las funciones normalizadas son de la forma y aparecen en la función de onda del átomo de hidrógeno. Abajo se listan las primeras pocas funciones de Legendre asociadas. Las funciones de Legendre asociadas se pueden usar para construir otro conjunto importante de funciones, las armónicas esféricas.

Índice Referencias Kreyszig Sec 4.3 Leighton Cap. 5

HyperPhysics*****HyperMath*****Cálculo M Olmo R Nave

Atrás