Problema de la Ley del Inverso del Cuadrado

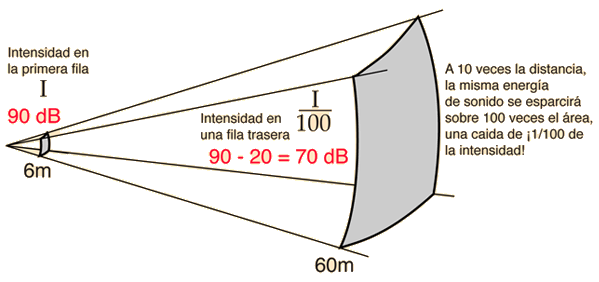
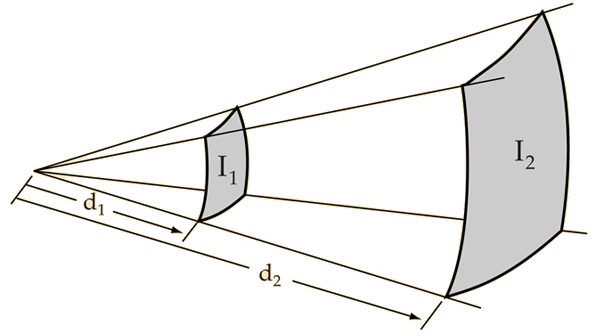
En un área abierta, el sonido disminuye de acuerdo con la ley del inverso del cuadrado. En un auditorio donde los asientos delanteros están a 6 metros (20 pies) de la fuente de sonido, y los asientos traseros están a 60 m (200 pies) de la fuente de sonido, la intensidad del sonido, si sigue este patrón, caerá por un factor de 100 ( = 20 decibelios ), entre los asientos delanteros y los traseros. Esto es una pérdida inaceptable, que se impide parcialmente por la reverberación.

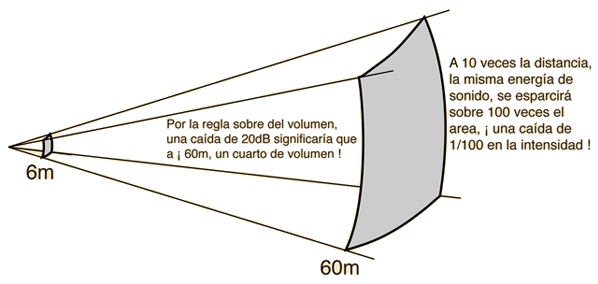
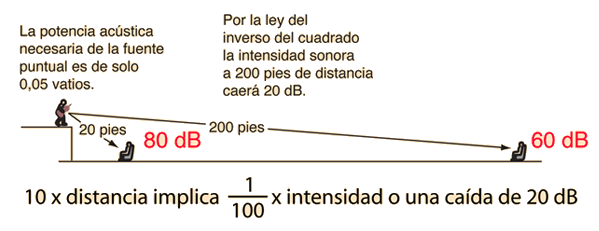
Para un sonido en el rango medio de la audición humana, se puede anticipar que se experimentará una caida de 20 db, aproximadamente un cuarto de su fuerza (regla de oro del volumen de sonido). Pero para sonidos en el rango inferior de la audición humana, como en el extremo inferior de la escala del piano, la pérdida en el volumen efectivo es aún mas severa, debido a la pérdida progresiva de las bajas frecuencias del oído humano. Esto produce otro problema en la acústica del auditorio llamado problema de pérdida de bajos.

Ejemplo de la Ley del Inverso del Cuadrado

Si se produc un nivel sonoro de 90 decibelios en la primera fila de un auditorio, y la última fila está 10 veces más lejos, entonces si se aplica la ley del inverso del cuadrado la intensidad del sonido se reducirá en un factor de 100. Un factor de 100 es una caída de 20 decibelios, se tiene pues un nivel de 70 decibelios en la fila posterior. 90 dB es un sonido fuerte que se le asigna un nivel dinámico ff , pero 70 dB es un sonido suave medio de nivel dinámico mp.

Ley del Inverso del Cuadrado en Ratio

Expresada como ratio, la ley del inverso del cuadrado toma la forma

Si d2 = x d1 entonces I2 = I1/( ) = I1

Si I1 = dB, entonces I2 = dB

Se puede explorar numericamente para confirmar que doblando la distancia, la intensidad cae unos 6 dB y que a 10 veces la distancia, la intensidad cae en 20 dB.