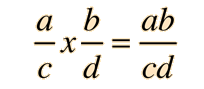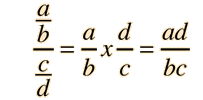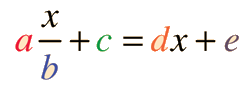Propiedades Algebráicas de los Números RealesLas propiedades algebráicas básicas de los números reales a,b y c son: 1. Cerradura: a + b y ab son números reales2. Commutativa: a + b = b + a, ab = ba 3. Asociativa: (a+b) + c = a + (b+c), (ab)c = a(bc) 4. Distributiva: (a+b)c = ac+bc 5. Identidad: a+0 = 0+a = a 6. Inverso: a + (-a) = 0, a(1/a) = 1 7. Cancelación: Si a+x=a+y, entonces x=y 8. Factor cero: a0 = 0a = 0 9. Negación: -(-a) = a, (-a)b= a(-b) = -(ab), (-a)(-b) = ab |
Índice | ||
|
Atrás |
Combinaciones AlgebráicasSumandos con un denominador común, se pueden expandir: Se pueden sumar fracciones reduciéndolas a denominador común:  Los productos de fracciones se pueden llevar a cabo directamente:  El cociente entre fracciones se lleva a cabo invirtiendo el denominador y aplicando el producto:  |
Índice | ||
|
Atrás |
Ecuaciones AlgebráicasEl papel de una ecuación algebráica básica es, proporcionar una formulación matemática formal sobre un problema lógico. Una ecuación algebráica de primer orden debería contener una cantidad desconocida y los demás términos conocidos. La tarea de una ecuación algebráica es aislar la cantidad desconocida en un lado de la ecuación, para evaluarla numericamente. Usando x como la cantidad desconocida (incógnita) y otras letras para representar las conocidas, consideramos el siguiente ejemplo de ecuación:  La estrategia para resolver esta ecuación consiste en la aplicación repetida de la regla de oro del álgebra para juntar todos los términos semejantes, y aislar la incógnita en un lado de la ecuación.  |
Índice | ||
|
Atrás |
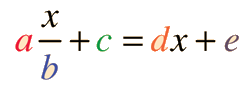
Ecuación Práctica AlgebráicaLa estrategia para resolver una ecuación algebráica básica, consiste en la aplicación repetida de la regla de oro del álgebra para aislar la incógnita en un lado de la ecuación. Usando x para representar la incógnita y otras letras para representar las cantidades conocidas, consideremos el siguiente ejemplo de ecuación:Notemos que hay determinadas circunstancias, donde no existe una solución. Si b=0, entonces el primer término se hace infinito. Por tanto, si no introducimos cantidad en b, el valor preestablecido es 1 con objeto de evitar la condición de infinito. Cualquier conjunto de valores que sean a=bd también dará infinito, como puede comprobarse en el cálculo de x de arriba. |
Índice | ||
|
Atrás |
Regla de Oro del ÁlgebraSobre un lado de la ecuación podemos realizar cualquier operación matemática, siempre que sobre el otro lado se realice la misma operación.La solución de la ecuación algebráica básica, se consigue aplicando repetidamente esta regla, con objeto de aislar la incógnita y evaluarla. La aplicación de esta regla -realizar claras operaciones simétricas sobre ambos lados de la ecuación-, puede ayudarnos a evitar los errores comunes que se cometen al resolver las ecuaciones algebráicas. 
|
Índice | ||
|
Atrás |