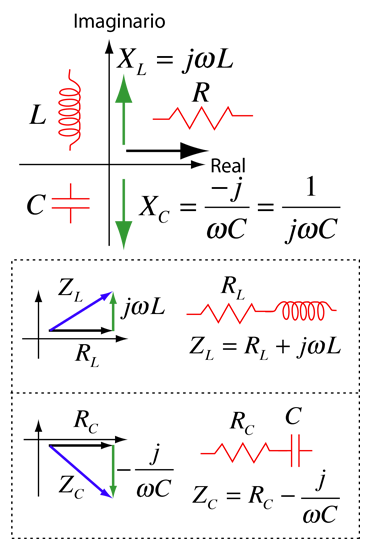
Use of Complex Impedance
El manejo de la impedancia de un circuito de corriente alterna con múltiples componentes se convierte rápidamente en un asunto inmanejable si para representar los voltajes y las corrientes, se utilizan los senos y cosenos. Una construcción matemática que rompe esa la dificultad es el uso de funciones exponenciales complejas. Las partes básicas de esta estrategia son las siguientes:
|
| 
| Forma Polar de Número Complejo | |
|
|  | ||
|
| 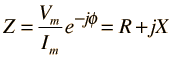 | Combinaciones de Impedancias | Diagrama Fasor |
|
| 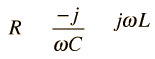 | Combinaciones RL y RC | Ejemplo de Elementos Paralelos |
Conceptos sobre Circuitos AC
| HyperPhysics*****Electricidad y Magnetismo | M Olmo R Nave |