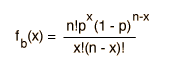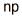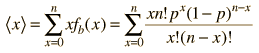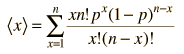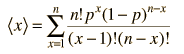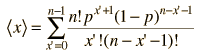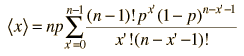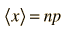El Valor Esperado
El valor que se espera obtener de un experimento estadístico se llama el valor esperado. Tambien llamado "esperanza matemática". Tambien lo llamamos "media" y esta es la palabra que vamos a seguir usando. Si tiramos una moneda 10 veces, esperamos que salga 5 veces "cara" y 5 veces "cruz". Esperamos obtener este valor porque la probabilidad de que salga "cara" es 0,5, y si lanzamos la moneda 10 veces, obtenemos 5. Por lo tanto, 5 es la media. Para formalizar este particular ejemplo de la media, si p es la probabilidad y n el número de eventos, la media es a = np. Esta es la forma de la media cuando se puede expresar la probabilidad por medio de la distribución binomial.
Para formalizar el concepto un poco mas, en un experimento con resultados discretos xi para los cuales la probabilidad es P(xi), la media estará dada por
a = ΣxiP(xi)
En el caso de variables continuas donde se expresa la probabilidad en términos de una función de distribución, la media toma la forma
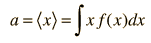
Conceptos de Estadística Aplicada
| HyperPhysics*****HyperMath*****Álgebra | M Olmo R Nave |