Demostraciones del Momento Angular
El tema de la mecánica depende en gran medida de las leyes de conservación, tales como la conservación de la energía, la conservación del momento, y la conservación del momento angular. Las dos primeras demostraciones muestran la conservación del momento angular, y la tercera muestra la naturaleza vectorial del momento angular cuando un par desequilibrado actúa sobre el sistema.
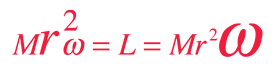 Como ejemplo de la mecánica del momento angular, el giro sobre un taburete con masas extendidas demuestra la conservación del momento angular. Al llevar las masas hacia el centro hace que el taburete gire más rápido. El momento angular es igual al momento de inercia multiplicado por la velocidad angular, por lo que si se reduce el momento de inercia en un factor de dos tirando de las masas hacia adentro, la velocidad de giro se duplicará. |  |
 | Otra forma de demostrar la conservación del momento angular es hacer girar una rueda y sostenerla en el taburete giratorio. Si gira la rueda para invertir la dirección de su momento angular, entonces el taburete girará en sentido contrario para mantener igual el momento angular del vector. En el caso ideal de que no haya par de fricción del taburete, el momento angular total del sistema debe permanecer igual tanto en magnitud como en dirección. |
Si una rueda giratoria se apoya en un punto del eje para que haya un par neto sobre él, el par cambiará el momento angular de una manera llamada "precesión". Tanto el momento angular como el par son cantidades vectoriales, y si el par aplicado tiene un componente perpendicular al momento angular, producirá una tasa de cambio de dirección del eje de rotación. | 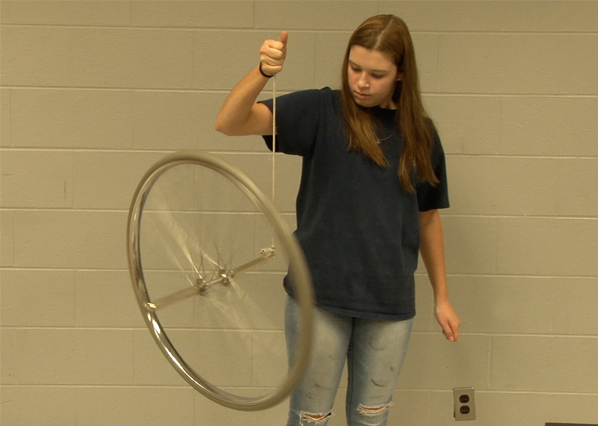 |
Conservación del Momento Angular
| HyperPhysics*****Mecánica | M Olmo, J Nave, R Nave |