La Rueda de Bicicleta
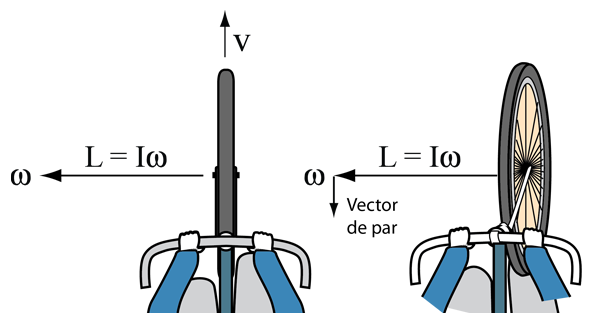
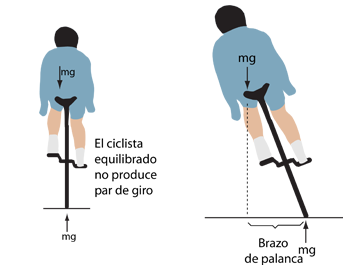
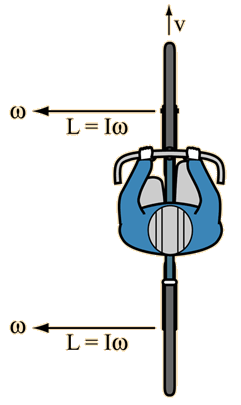
| El momento angular de las ruedas de bicicleta girando, las hace actuar como giroscopios que ayudan a estabilizar la bicicleta. Esta acción giroscópica, tambien ayuda a rodar la bicicleta. Tras recordar la naturaleza giroscópica de la rueda de la bicicleta, hay que señalar que los experimentos indican que esa estabilidad giroscópica derivada de las ruedas no es una parte importante de la estabilidad total de la bicicleta. Los momentos de inercia y la velocidad tampoco son suficientemente grande. Los experimento y revisiones de Lowell y McKell indican que la estabilidad de la bicicleta se puede describir en términos de fuerza centrífuga. Un ciclista que sienta un desequilibrio a la izquierda girará el manillar hacia la izquierda, produciendo un segmento de trayectoria circular cuya fuerza centrífuga resultante empuja la parte superior de la bicicleta a regresar hacia la posición vertical a una condición de equilibrio. Probablemente las mayores masas y velocidades de las ruedas de las motos, producen pares giroscópicos mayores que sí afectan considerablemente a la estabilidad en el caso de las motocicletas. |
 |
Ejemplos de Vectores de Rotación
Referencia
Lowell and McKell
| HyperPhysics*****Mecánica*****Movimiento Rotacional | M Olmo R Nave |