Puntos Lagrange del Sistema Tierra-Sol

Un sistema mecánico con tres objetos, digamos Tierra, Luna y Sol, constituye un problema de tres cuerpos. El problema de tres cuerpos es y sigue siendo famoso en los círculos físico y matemático. Finalmente en la década de 1950, se logró una elegante prueba de que es un problema imposible de resolver. Sin embargo, pueden ser muy útiles soluciones aproximadas, particularmente cuando las masas de los tres objetos son muy diferentes.

Los matemáticos del siglo 18 Leonhard Euler y Joseph-Louis Lagrange descubrieron que había cinco puntos especiales en este marco de referencia giratorio, donde podría mantenersee un equilibrio gravitacional. Estos cinco puntos fueron llamados puntos de Lagrange y numerados de L1 a L5. Es decir, un objeto colocado en cualquiera de estos cinco puntos del marco de referencia giratorio se quedaría allí, con todas las fuerzas efectivas cancelándose entre sí. Los puntos de Lagrange se pueden visualizar como superficies equipotenciales de tres cuerpos. Los objetos colocados en los puntos de Lagrange del sistema Tierra-Luna se podrían mantener allí y entonces orbitar alrededor del Sol, manteniendo la misma posición relativa con respecto al sistema Tierra-Luna.

En los últimos años una serie de misiones de satélites de exploración espacial han hecho uso de los puntos de Lagrange Tierra-Sol para el posicionamiento de los satélites de observación. El diagrama de abajo presenta la geometría general, pero la gran diferencia de masa entre el Sol y la Tierra hace que sea difícil dibujar a escala los puntos de Lagrange Tierra-Sol. Mientras que L3 estaría en el lado opuesto del Sol y por lo tanto obviamente no sería útil, los puntos de Lagrange L1 y L2 se han utilizado para los satélites de observación.

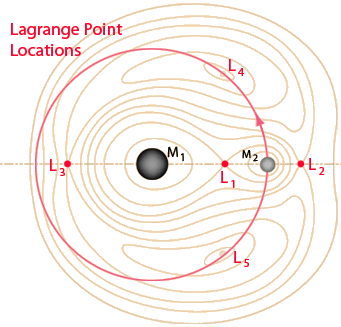Los puntos de Lagrange L4 y L5 constituyen puntos de equilibrio estable, de manera que un objeto colocado allí se mantendría en una órbita estable con respecto a M1 y M2. Las pequeñas desviaciones afuera de L4 o L5, originarían una fuerza de recuperación efectiva que llevaría al satélite de nuevo al punto estable.

Los puntos de Lagrange L1, L2 y L3 no parecen ser tan útiles, ya que son puntos de equilibrio inestable. Al igual que el equilibrio de un lápiz sobre su punta, el manteniendo de un satélite es teóricamente posible, pero cualquier influencia perturbadora lo conduciría fuera del equilibrio. Sin embargo, en la práctica, estos puntos de Lagrange han demostrado ser muy útiles. De hecho se puede hacer una nave espacial que ejecute una pequeña órbita alrededor de uno de estos puntos de Lagrange con muy pequeño gasto de energía. Estos puntos han proporcionado lugares útiles para el "aparcamiento" de una nave espacial para las observaciones. Estas órbitas alrededor de L1 y L2 son a menudo llamadas "órbitas de halo".

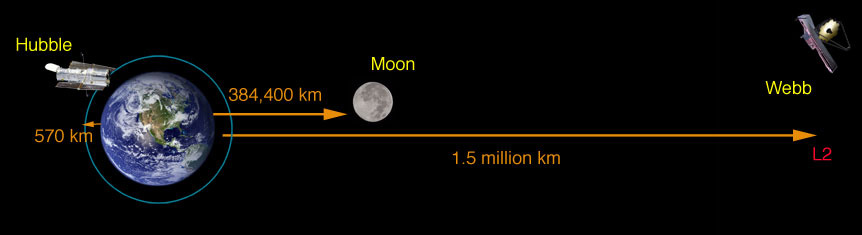
El punto de Lagrange Tierra-Sol L2 se ha utilizado para la Wilkinson Microwave Anisotropy Probe (WMAP), Sonda de Anisotropía de Microondas Wilkinson). L2 está posicionada fuera de la órbita de la Tierra de manera que la WMAP siempre está encarada afuera tanto del Sol como de la Tierra, una característica importante para una sonda de espacio profundo, que puede emplear detectores ultrasensibles, sin el peligro de que sean "cegados" observando el Sol o la Tierra.

Este punto L2 también se utilizó para el satélite Planck para el estudio del Fondo Cósmico de Microondas, y se utilizará para el Telescopio Espacial James Webb.

El punto de Lagrange del sistema Tierra-Sol L2, está situado hacia el exterior de la Tierra alrededor del 1% de la distancia Tierra-Sol.

Imágenes de la NASA

Referencias:

Wiki Puntos de Lagrange

WMAP en el Punto Lagrange L2

Joseph Louis Lagrange

Lagrange fue un matemático del siglo 18 que abordó el famoso "problema de los tres cuerpos" a finales de 1700. El problema no se puede resolver con exactitud, pero él encontró que en el caso en el que el tercer cuerpo es muy pequeño en comparación con los otros dos, se podían encontrar algunas soluciones aproximadas útiles.