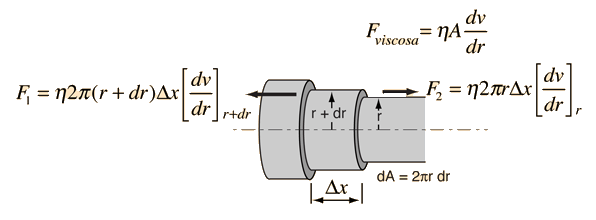
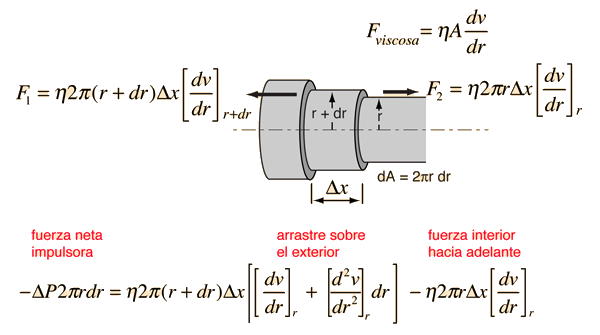
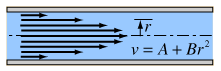
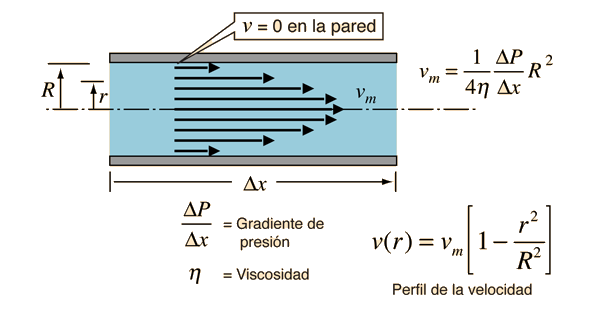
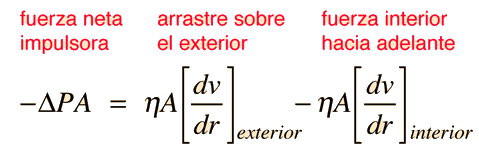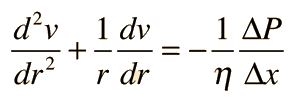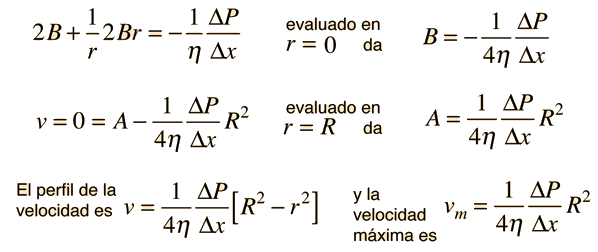Energía Cinética del Flujo del Tubo
Para obtener la energía cinética de un flujo laminar en un tubo, se debe tomar en consideración el promedio del cuadrado de la velocidad para el perfil de la velocidad.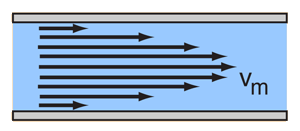 |
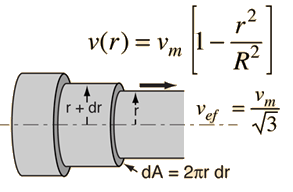 |
El promedio del cuadrado de la velocidad está dado por
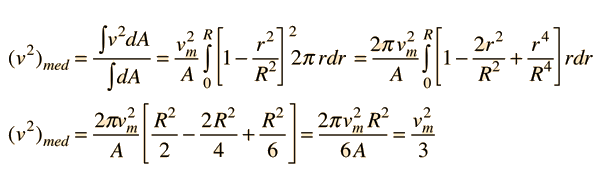
El promedio de energía cinética por unidad de volúmen, se puede expresar en términos de la densidad del fluido r y la velocidad de flujo máxima vm.

Conceptos sobre la Ley de Poisuille
| HyperPhysics*****Mecánica*****Fluidos | M Olmo R Nave |