Intensidad de Difracción por Rendija Simple
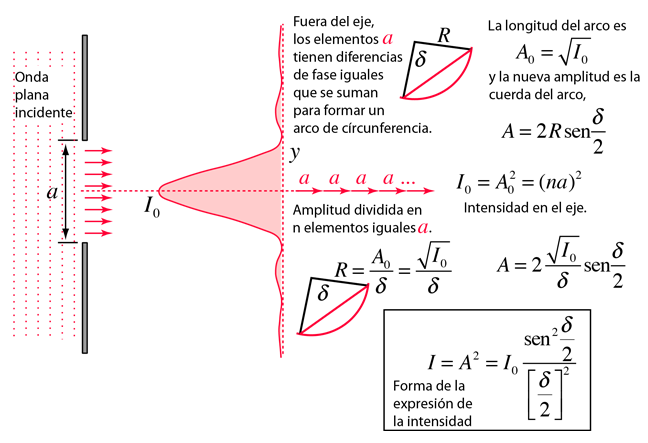
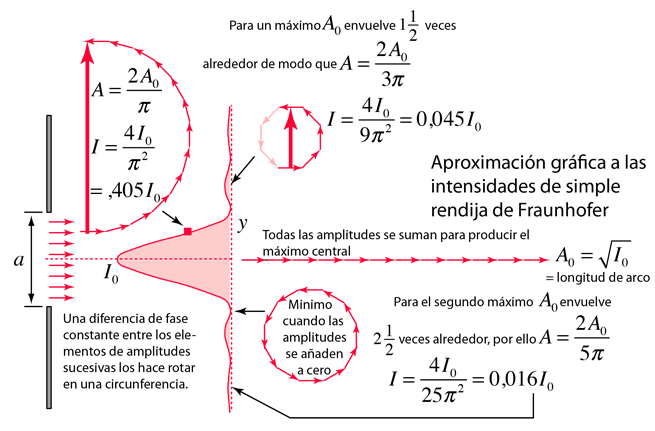
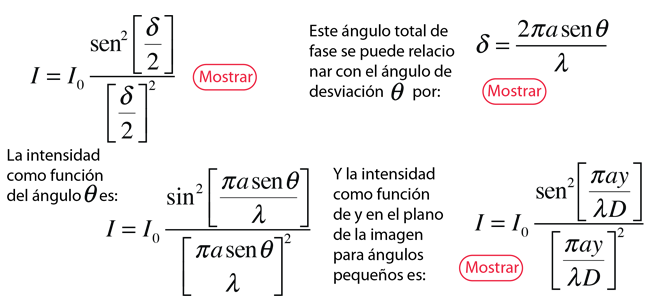
Bajo las condiciones de Fraunhofer, las ondas que llegan a la rendija simple son ondas planas. Dividida en segmentos, cada uno de ellos se puede considerar como fuentes puntuales. Las amplitudes de los segmentos tendrán un desplazamiento de fase constante respecto del adyacente y cuando se sumen como vectores, formarán segmentos de un arco circular. La intensidad relativa resultante, dependerá del desplazamiento de fase total δ de acuerdo con la siguiente fórmula:
Conceptos de Difracción
Difracción de Fraunhofer
Conceptos de Intensidad de Fraunhofer
| HyperPhysics*****Luz y Visión | M Olmo R Nave |