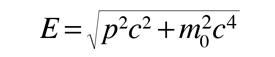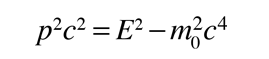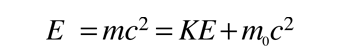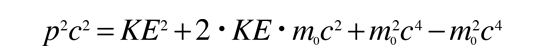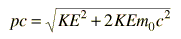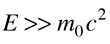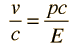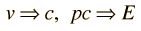Longitud de Onda de DeBroglie

Una forma adecuada para la expresión de la longitud de onda de De Broglie es

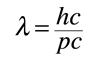donde hc = 1239,84 eV nm, y pc se expresa en electrón voltios.

Esto es particularmente apropiado para la comparación con las longitudes de onda de los fotones, ya que para el fotón, pc=E, y un fotón de 1 eV, se ve inmediatamente que tiene una longitud de onda de 1240 nm. Para partículas masivas con energía cinética KE, que sea mucho menor que su energía de masa en reposo:

...

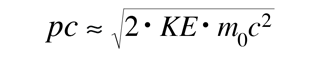Mostrar

Para un electrón con KE = 1 eV, y una energía de masa en reposo de 0,511 MeV, la longitud de onda de DeBroglie asociada es de 1,23 nm, alrededor de un millar de veces más pequeña que un fotón de 1 eV. (Esta es la razón por la que la resolución limitante de un microscopio electrónico, es mucho mayor que la de un microscopio óptico.)

El cálculo siguiente utiliza las expresiones relativistas completas para la energía cinética, etc

¡Precaución!: Dado que este cálculo fue diseñado para velocidades que son una fracción significativa de la velocidad de la luz, puede perder algo de precisión para velocidades muy bajas. Bajo aquellas condiciones, se produce en el cálculo pequeñas diferencias entre grandes números. En los cálculos de baja velocidad como el ejemplo de la pelota de béisbol, tal vez sería más exacto utilizar el cálculo no relativista.

Utilidad de la Cantidad pc

La expresión de la energía relativista de una partícula es:

que se reduce a E = pc, en los fotones . La cantidad pc es proporcional al momento relativista, pero tiene unidades de energía, y es de utilidad en muchos cálculos de alta energía. Utilizando

y

se puede obtener una expresión de pc en términos de la energía cinética relativista:

En los procesos más comunes, la energía cinética es mucho menor que la energía de masa en reposo, por lo que generalmente se puede despreciar el primer término. Esto lleva a la aproximación útil:

Para energías de electrones inferiores a 20 keV y energías de protones inferiores a 38 MeV, esta expresión tiene un error menor del 1%.

Para velocidades relativistas extremas dónde

entonces

Para menos de un 1% de error, esto requiere energías de electrones de más de 3,2 MeV, y energías de protones de más de 5,8 GeV.

Una aplicación útil de la cantidad pc, se da en el cálculo de la velocidad como fracción de c.

y como