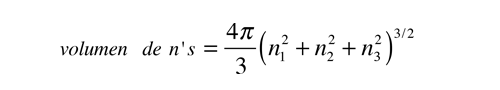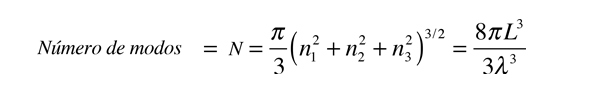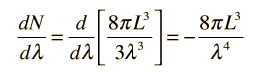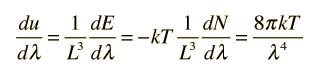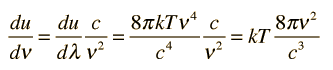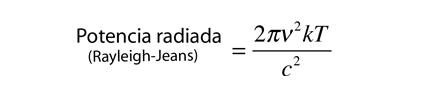Ondas Electromagnéticas en una Cavidad Cúbica

Las ondas electromagnéticas estacionarias en una cavidad que está en equilibrio con su entorno, no pueden tomar un camino cualquiera. Deben satisfacer la ecuación de ondas en tres dimensiones:

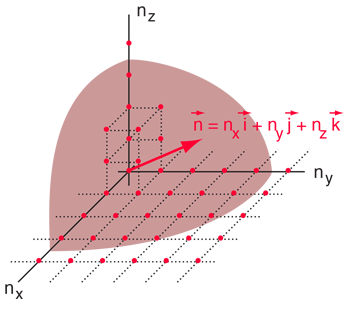
La solución de la ecuación de onda, debe dar una amplitud cero en las paredes, ya que un valor distinto de cero sería disipar energía, y violaría la suposición de equilibrio. Para formar una onda estacionaria, la trayectoria de la reflexión alrededor de la cavidad, deben ser una trayectoria cerrada. Las condiciones de contorno pueden ser satisfechas con una solución de la forma:

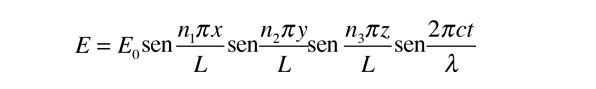
Sustituyendo esta solución a la ecuación de onda anterior da

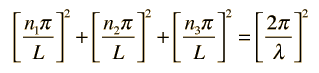
que se simplifica a

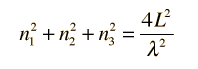
¿Cuantos Modos en la Cavidad?

Esquema de Rayleigh para el conteo de modos. De Richtmyer, et al.

Es necesario evaluar el número de modos que pueden cumplir esta condición, lo que equivale a contar todas las posibles combinaciones de los valores enteros n. Se puede hacer una aproximación tratando el número de combinaciones como el volumen de una cuadrícula tridimensional de los valores de n, un "espacio-n". Utilizando la fórmula del volumen de una esfera, con los valores n especificando las coordenadas a lo largo de tres ejes "n", da

Sin embargo, esto conlleva un par de problemas. Al utilizar la esfera, se han usado valores de n tanto positivos como negativos, mientras que la solución de la ecuación de onda, utiliza solamente definidos valores positivos. Por lo tanto hay que tomar 1/8 del volumen anterior. Otro problema técnico es que se pueden tener ondas polarizadas en dos planos perpendiculares, por lo que debemos multiplicar por dos para dar cuenta de ello. Luego, se puede tomar el volumen como una medida del número de modos, convirtiéndose en una muy buena aproximación, cuando el tamaño de la cavidad es mucho mayor que la longitud de onda, como en el caso de ondas electromagnéticas en una cavidad finita. Utilizando la relación obtenida para los valores de n, esto se convierte en

¿Cuantos Modos por Unidad de Longitud de Onda?

Después de haber desarrollado una expresión para el número de modos de ondas estacionarias en una cavidad, se podría conocer la distribución con la longitud de onda. Esto puede obtenerse tomando la derivada de la cantidad de modos con respecto a la longitud de onda.

El signo negativo aquí, revela que el número de modos disminuye con la longitud de onda creciente. Ahora, para obtener el número de modos por unidad de volumen por unidad de longitud de onda, simplemente se puede dividir por el volumen de la cavidad cúbica.

Téngase en cuenta que esto ¡no implica la aproximación de una esfera con un cubo! La esfera se utilizó para calcular el número de modos que había en una esfera en el "espacio-n", lo que permite contar el número de modos posibles. Además, el uso de una cavidad cúbica en el cálculo, permite reducir la complejidad geométrica del desarrollo, pero el resultado final obtenido es independiente de la geometría de la cavidad.

¿Cuanta Energía por Unidad de Volumen?

La asignación de energías a las ondas estacionarias electromagnéticos en una cavidad, se basa en el principio de equipartición de energía. Cada modo de onda estacionaria, tendrá una energía media kT, donde k es la constante de Boltzmann y T es la temperatura en grados Kelvin. Representando u como la densidad de energía:

Esta es una relación importante en la teoría clásica de la cavidad electromagnética. También se puede expresar en términos de la frecuencia ν, haciendo uso de la regla de la cadena y la relación de onda:

El signo menos aquí, sólo recuerda que una disminución de la longitud de onda implica un aumento de la frecuencia. La magnitud de la dependencia de la densidad de energía sobre la frecuencia, está dada por:

Téngase en cuenta que este es el resultado clásico que se utilizó en la ley de Rayleigh-Jeans, pero que conduce a la catástrofe ultravioleta. Produce un buen acuerdo en el límite de baja frecuencia, pero para las frecuencias más altas se debe utilizar la fórmula de la radiación de Planck.

Energía Radiada como Función de la Longitud de Onda

Si se considera la energía radiada perpendicular a un pequeño incremento de área, entonces, hay que señalar que si el sistema está en equilibrio térmico, la mitad de la densidad de energía de las ondas se va hacia las paredes, y la mitad sale. La evaluación de la potencia vista en un punto de observación, requiere una consideración de la geometría:

pero a un ángulo θ, el área efectiva será Acosθ, y la velocidad efectiva será c cosθ, por lo que la energía radiada se reducirá a

Para un punto de observación cerca de la superficie radiante, la potencia será la potencia media de todas las direcciones, y el promedio da otro factor de 1/2.

Después de haber promediado sobre todos los ángulos, la potencia radiada calculada por unidad de longitud de onda, es finalmente

Esta es la fórmula de Rayleigh-Jeans. El hecho de que fallara en la predicción de la distribución espectral de objetos calientes, era uno de los principales problemas no resueltos de la física a principios del siglo 20.
Para expresarlo en términos de la frecuencia, se realiza una aplicación de la regla de la cadena como se hizo anteriormente con la densidad de energía, dando una potencia radiada por unidad de frecuencia: