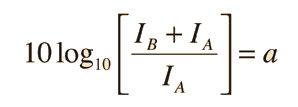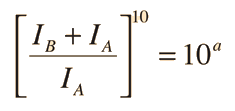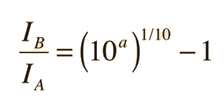Enmascaramiento

Esta frase lleva la esencia de la sabiduría popular sobre el enmascaramiento del sonido. Los sonidos de baja frecuencia, amplias bandas (como el agua corriendo) enmascaran los sonidos más altos de frecuencia que son más suaves al oído del oyente (como un tono de conversación en una sala). Para un tono de enmascaramiento de frecuencia única, puede determinarse experimentalmente las curvas de enmascaramiento. Asimismo, por la idea de la diferencia apenas perceptible (JPN) de la intensidad del sonido, se puede calcular aproximadamente la cantidad a añadir de un segundo sonido, que podría exceder el jpn, y por tanto hacerse audible.

El ruido blanco de banda ancha tiende a enmascarar todas las frecuencias, y es aproximadamente lineal en el enmascaramiento. Por lineal, significa que si se eleva el ruido blanco en 10 dB, hay que elevar todos los demas, otros 10 dB para oirlo.

Curvas de Enmascaramiento

Se muestran los efectos de enmascaramiento, de tonos de 1200 Hz de varias intensidades. Nótese que es eficaz para enmascarar sonidos de frecuencia por encima de ella, pero no por debajo. Las caídas a 1200 y 2400 provienen de los efectos de batidos.

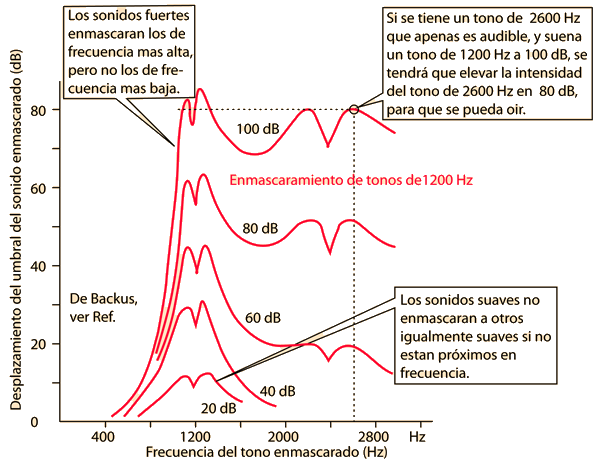
Backus atribuye estos datos a Harvey Fletcher en "Speech and Hearing in Communication", pag.155

Aunque el enmascaramiento es un fenómeno complejo, la experiencia de enmascarar sonidos de frecuencia más alta con fuertes sonidos de baja frecuencia, es una experiencia común y de gran importancia en la orquestación. Es fácil crear circunstancias en las que una fuerte sección de bajos de metal, puede enmascarar los sonidos más suaves de frecuencias más altas de la sección de vientos de madera.

Umbral de Audición, Segundo Sonido

Si se toma la diferencia apenas perceptible (JPD) general de la intensidad de un sonido como 1 decibelio, entonces, para que se oyese la adición de un segundo sonido, tendría que elevar la intensidad total en 1 dB. Esto es aproximadamente un aumento del 25%, de modo que el segundo sonido debería tener sobre 1/4 de la intensidad, o unos 6 dB menos que el existente, enmascarando el sonido. Aunque este enfoque no es un tratamiento adecuado del complejo tema del enmascaramiento, permite calcular la cantidad necesaria de un segundo sonido, para cumplir cualquier criterio que se establezca en términos de aumento de decibelios en un campo sonoro.

Detalles del Cálculo, Umbral de Enmascaramiento

Si la cantidad de sonido B que se debe añadir a un sonido preexistente A aumenta el nivel de decibelios general en una cantidad a en decibelios, ese requerimiento se puede establecer como

Resultando el ratio de las dos intensidades

Este ratio en decibelios se puede restar del nivel I_A en dB para obtener el umbral de I_B que podría justamente oirse.