La Entropía como Medida de la Multiplicidad de un Sistema

La probabilidad de encontrar un sistema en un estado determinado depende de la multiplicidad de ese estado. Es decir, es proporcional al número de maneras en que se puede producir ese estado. Aquí un "estado" es definido por alguna propiedad medible que permita distinguirlo de otros estados. En el lanzamiento de un par de dados, la propiedad medible, es la suma de la cantidad de puntos boca arriba. La multiplicidad de mostrar dos puntos es sólo uno, porque sólo hay una disposición de los dos dados que nos dará ese estado. La multiplicidad de mostrar siete puntos es de seis, porque con los dos dados hay seis arreglos que muestran un total de siete puntos.

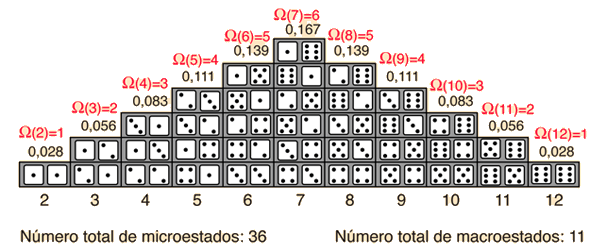
Una forma de definir la cantidad "entropía" es hacerlo en función de la multiplicidad.

donde k es la constante de Boltzmann. Esta es la expresión de Boltzmann para la entropía, y de hecho S = klnΩ está tallada en su lápida! La k se incluye como parte de la definición histórica de entropía y proporciona las unidades Joule / Kelvin en el sistema de unidades SI. Se utiliza el logaritmo para hacer que la entropía definida tenga un tama–o razonable. También proporciona el tipo de comportamiento correcto para combinar dos sistemas. La entropía de los sistemas combinados será la suma de sus entropías, pero la multiplicidad será el producto de sus multiplicidades. El hecho de que el logaritmo del producto de dos multiplicidades sea la suma de sus logaritmos individuales, da el tipo adecuado de combinación de entropías. La multiplicidad para colecciones ordinarias de materia es inconvenientemente grande, del orden del nœmero de Avogadro, por lo que es conveniente usar para la entropía el logaritmo de la multiplicidad

En un sistema con un gran número de partículas, como una mol de átomos, el estado más probable será abrumadoramente probable. Se puede esperar con confianza que el sistema en equilibrio, se encontrará en el estado de máxima multiplicidad, ya que por lo general, las fluctuaciones de ese estado serán demasiado pequeñas para ser medidas. Cuando un sistema grande alcanza el equilibrio, su multiplicidad (entropía) tiende a aumentar. Esta es una forma de establecer la segunda ley de la termodinámica.

Entropía en Términos de Calor y Temperatura

La fórmula que originalmente se usó para definir la entropía S es

Si no se necesita conocer los detalles microscópicos, esto es a menudo una definición de entropía suficiente. Se puede integrar para calcular el cambio en la entropía durante una parte de un ciclo de motor. En el caso de un proceso isotérmico, se puede evaluar simplemente por ΔS = Q/T.

En este contexto, el cambio en la entropía se puede describir como el calor añadido por unidad de temperatura y sus unidades son los Julios/ºKelvin (J/K) o eV/ºK.