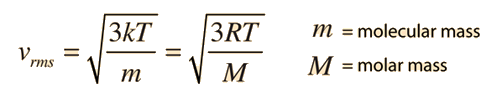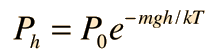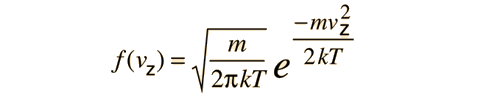Kinetic Temperature
The expression for gas pressure developed from kinetic theory relates pressure and volume to the average molecular kinetic energy. Comparison with the ideal gas law leads to an expression for temperature sometimes referred to as the kinetic temperature.

This leads to the expression

where N is the number of molecules, n the number of moles, R the gas constant, and k the Boltzmann constant. The more familiar form expresses the average molecular kinetic energy:
 |
|
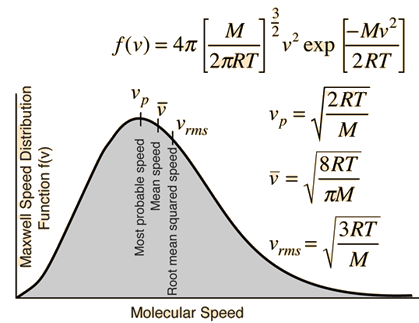
It is important to note that the average kinetic energy used here is limited to the translational kinetic energy of the molecules. That is, they are treated as point masses and no account is made of internal degrees of freedom such as molecular rotation and vibration. This distinction becomes quite important when you deal with subjects like the specific heats of gases. When you try to assess specific heat, you must account for all the energy possessed by the molecules, and the temperature as ordinarily measured does not account for molecular rotation and vibration. The kinetic temperature is the variable needed for subjects like heat transfer, because it is the translational kinetic energy which leads to energy transfer from a hot area (larger kinetic temperature, higher molecular speeds) to a cold area (lower molecular speeds) in direct collisional transfer.
| Define constants | Equipartition of energy | Thermal energy |
Gas law concepts
Kinetic theory concepts
| HyperPhysics***** Heat and Thermodynamics | R Nave |