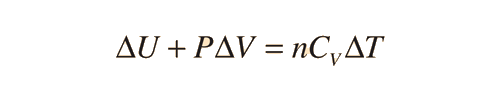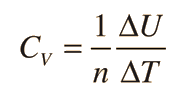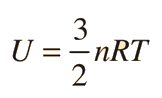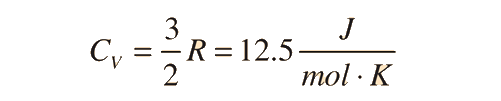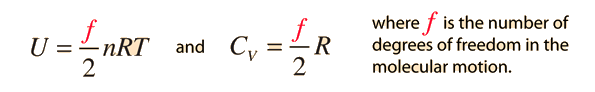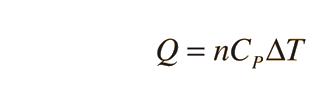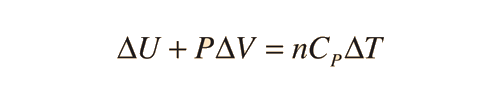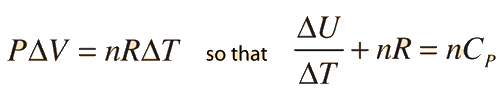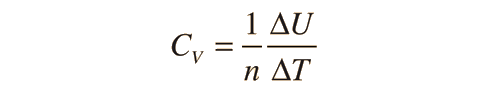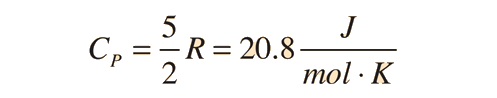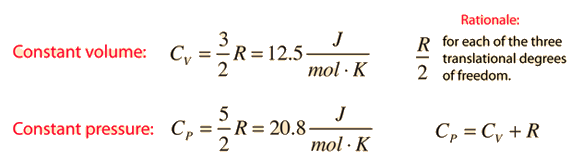Specific Heats of Gases
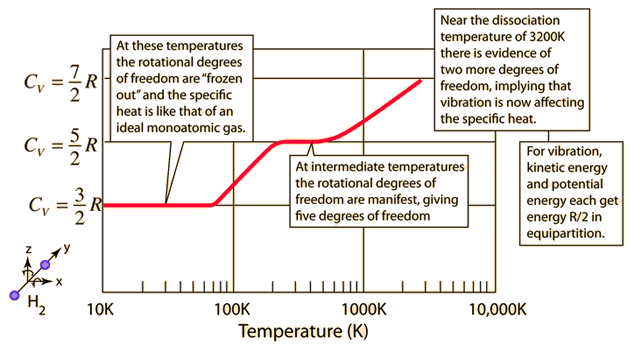
The specific heats of gases are generally expressed as molar specific heats. For a monoatomic ideal gas the internal energy is all in the form of kinetic energy, and kinetic theory provides the expression for that energy, related to the kinetic temperature. The expression for the internal energy is
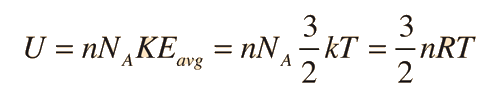
Two specific heats are defined for gases, one for constant volume (CV) and one for constant pressure (CP). For a constant volume process with a monoatomic ideal gas the first law of thermodynamics gives:
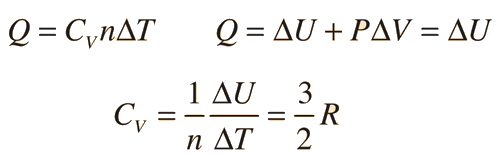 | More general case |
Further application of the ideal gas law and first law gives the relationship
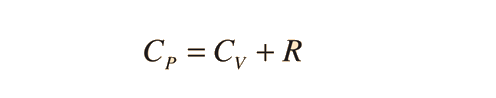 | Show |
The ratio of the specific heats γ = CP/CV is a factor in adiabatic engine processes and in determining the speed of sound in a gas. This ratio γ = 1.66 for an ideal monoatomic gas and γ = 1.4 for air, which is predominantly a diatomic gas.
Gas law concepts
Kinetic theory concepts
| HyperPhysics***** Thermodynamics | R Nave |