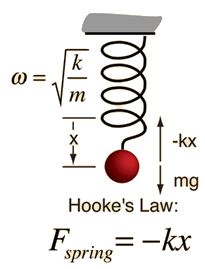
Simple Harmonic Motion Frequency
The frequency of simple harmonic motion like a mass on a spring is determined by the mass m and the stiffness of the spring expressed in terms of a spring constant k ( see Hooke's Law):

Periodic motion concepts
| HyperPhysics***** Mechanics | R Nave |