Big Bang Energy and Time Example
In Weinberg's First Three Minutes, the big bang expansion is modeled in segments which are characterized by time, temperature and characteristic particle energy. The first segment in which the process is so characterized, the temperature is 1011 Kelvin. Given that temperature, how do you calculate the associated time and particle energy?
The mean energy associated with a particle in thermal equilibrium at temperature T is kT, where k is the Boltzmann constant. So the characteristic particle energy at this temperature is
One important piece of information that we have is the energy density in the 3K background radiation, which is about 0.25 MeV/m3 at the present time. From the Stefan-Boltzmann law, we know that the energy density is proportional to T4, so we could scale the energy up to the temperature 1011 K. But this includes only the energy of the photons, and there are neutrinos, electrons and positrons also in thermal equilibrium at that time. The thermal energy at 8.6 MeV is so high compared to the pair-production threshold of about 1 MeV for the production of electron-positron pairs that it must be assumed that they are being continuously created. The collection of electrons and positrons is "radiation like", being in thermal equilibrium with the photons and neutrinos.
The known energy density of the photon background radiation can be scaled up to the target temperature and adjusted to include the neutrinos, electrons and positrons if we know the relative populations of each in the expanding big bang. At these high temperatures, those populations can be treated statistically, and the effective number of species of the particles established. Those populations relative to the photons are:
The energy density in the expanding big bang at 1011K can then be calculated:

Substituting this into Friedman's equation for the expansion time gives
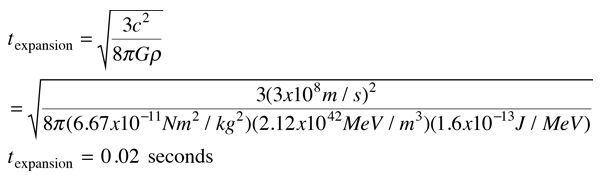
The next step in Weinberg's scenario has time 0.11 sec and temperature 3 x 1010K. If you just plug into the above relationship for that temperature, you get expansion time 0.24 seconds. I'm not clear on how you get 0.11 seconds.
| Temperature and expansion time |
Reference
Rohlf
Ch. 19
| HyperPhysics***** Astrophysics | R Nave |