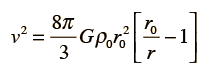Freefall Time and Star Formation Time
One of the classic problems of astronomy is the modeling of the gravitational contraction of a diffuse cloud of gas and dust to form a star. One step along the way to a realistic model is to calculate the freefall time. Starting with a simple model of a uniform spherical gas cloud, an element of mass m at the radius would experience a gravitational attraction as if the entire mass M were concentrated at the center. This follows from Gauss's law for the central, inverse square law force of gravity.
 | It is further assumed that there are no interactions between the particles other than gravity - i.e., no collisions or effective outward pressure. The dynamics of the contracting matter can then be described by Newton's second law. 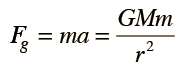 |
You can also in this context invoke conservation of energy so that the kinetic energy gained by the mass element m is equal to the change in gravitational potential energy.
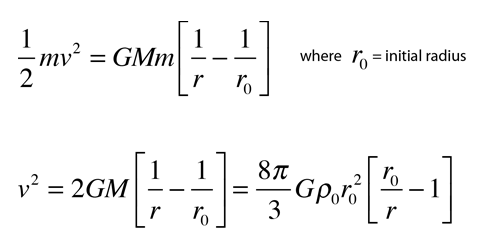
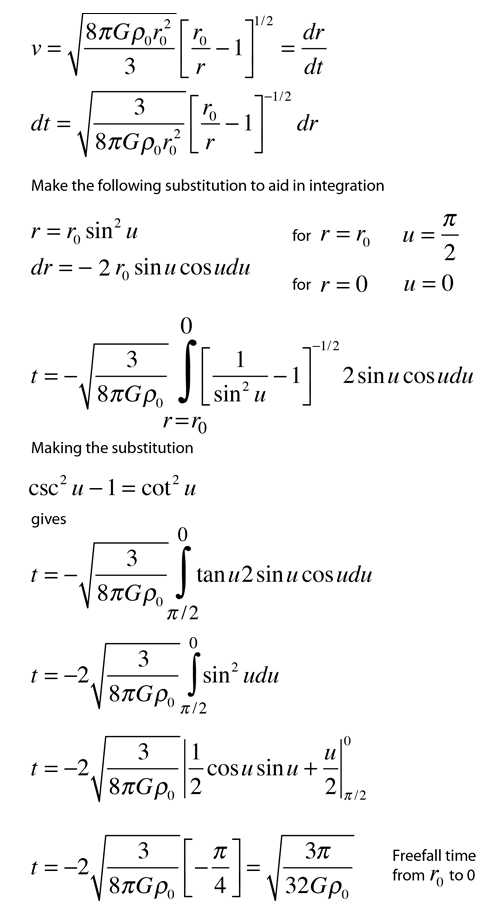
Integration of this expression to find the time to collapse to zero radius gives the freefall time expression.
 |
|
If the calculation is done with the solar parameters, you find that if all outward pressures and interactions were removed, the Sun would completely collapse in just under 30 minutes. This is not going to happen, but such modeling is nontheless useful to give insight into the brief time intervals associated with the collapse of the inner portions of stars, which may lead to supernova events.
Realistic star formation modeling must take into account collisions, pressure, temperature, radiation and other variables. Nevertheless, the freefall time is a useful parameter for modeling certain processes.
Star processes
Galaxy concepts
Reference
Harwit
Sec 12-15
Bowers & Deeming
Sec 1.3
| HyperPhysics***** Astrophysics | R Nave |