Conservation Laws
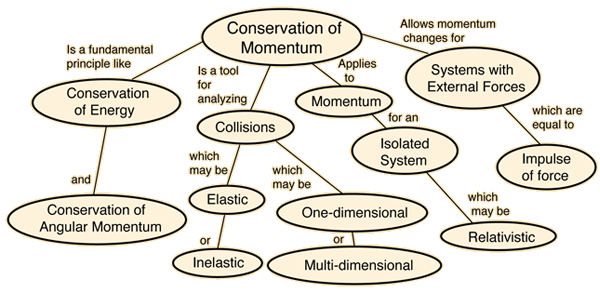
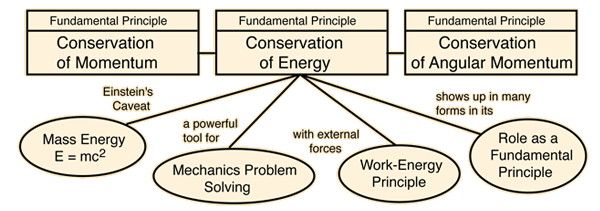
If a system does not interact with its environment in any way, then certain mechanical properties of the system cannot change. They are sometimes called "constants of the motion". These quantities are said to be "conserved" and the conservation laws which result can be considered to be the most fundamental principles of mechanics. In mechanics, examples of conserved quantities are energy, momentum, and angular momentum. The conservation laws are exact for an isolated system.

Stated here as principles of mechanics, these conservation laws have far-reaching implications as symmetries of nature which we do not see violated. They serve as a strong constraint on any theory in any branch of science. There are other types of conservation laws that govern the behavior of nature in the quantum realm.
| HyperPhysics***** Mechanics | R Nave |