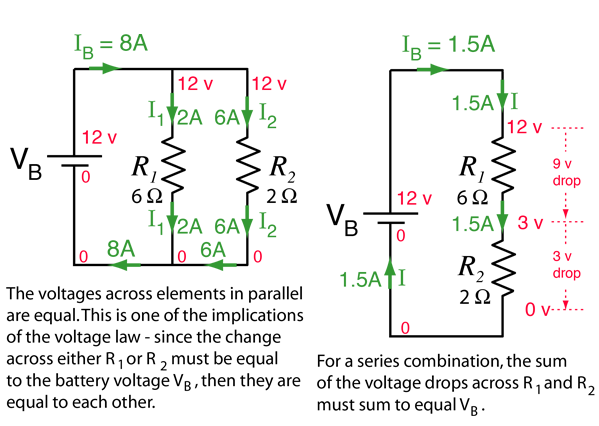
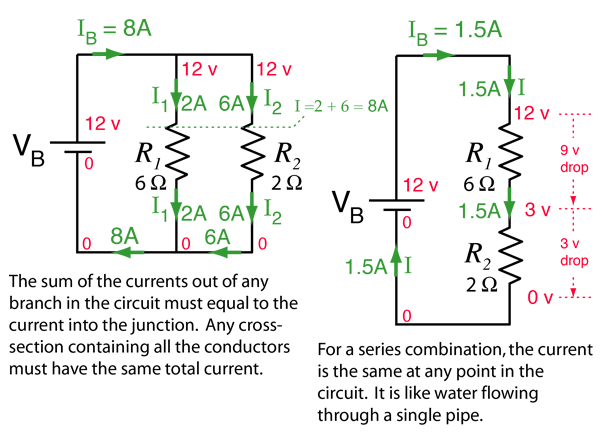
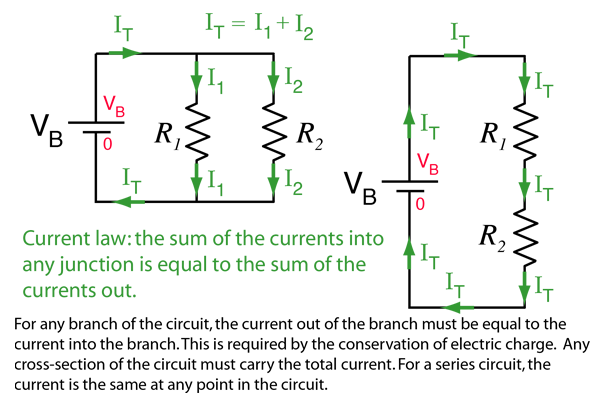Ohm's Law
For many conductors of electricity, the electric current which will flow through them is directly proportional to the voltage applied to them. When a microscopic view of Ohm's law is taken, it is found to depend upon the fact that the drift velocity of charges through the material is proportional to the electric field in the conductor. The ratio of voltage to current is called the resistance, and if the ratio is constant over a wide range of voltages, the material is said to be an "ohmic" material. If the material can be characterized by such a resistance, then the current can be predicted from the relationship:
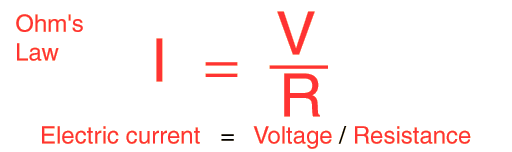
Data can be entered into any of the boxes below. Specifying any two of the quantities determines the third. After you have entered values for two, click on the text representing the third in the active illustration above to calculate its value.
| AC version of Ohm's law |
DC Circuits
| HyperPhysics***** Electricity and Magnetism | R Nave |