Rotational-Linear Parallels

| More comparisons between linear and angular motion |
Moment of inertia concepts
| HyperPhysics***** Mechanics ***** Rotation | R Nave |
Rotational-Linear Parallels
|
Index Moment of inertia concepts | ||
|
Go Back |
Rotational-Linear Parallels
|
Index Moment of inertia concepts | ||||
|
Go Back |
Moment of InertiaMoment of inertia is the name given to rotational inertia, the rotational analog of mass for linear motion. It appears in the relationships for the dynamics of rotational motion. The moment of inertia must be specified with respect to a chosen axis of rotation. For a point mass, the moment of inertia is just the mass times the square of perpendicular distance to the rotation axis, I = mr2. That point mass relationship becomes the basis for all other moments of inertia since any object can be built up from a collection of point masses. 
|
Index Moment of inertia concepts | ||||
|
Go Back |
Common Moments of Inertia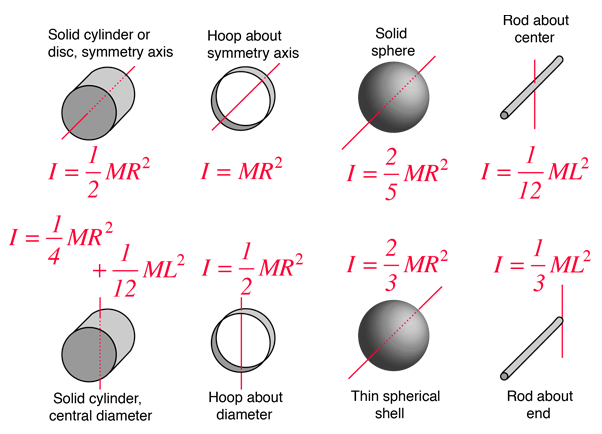 |
Index Moment of inertia concepts | ||
|
Go Back |
Moment of Inertia ExamplesMoment of inertia is defined with respect to a specific rotation axis. The moment of inertia of a point mass with respect to an axis is defined as the product of the mass times the distance from the axis squared. The moment of inertia of any extended object is built up from that basic definition. The general form of the moment of inertia involves an integral. 
|
Index Moment of inertia concepts | ||
|
Go Back |
Moment of Inertia, General FormSince the moment of inertia of an ordinary object involves a continuous distribution of mass at a continually varying distance from any rotation axis, the calculation of moments of inertia generally involves calculus, the discipline of mathematics which can handle such continuous variables. Since the moment of inertia of a point mass is defined by 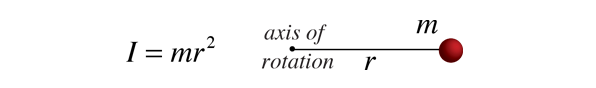 then the moment of inertia contribution by an infinitesmal mass element dm has the same form. This kind of mass element is called a differential element of mass and its moment of inertia is given by  Note that the differential element of moment of inertia dI must always be defined with respect to a specific rotation axis. The sum over all these mass elements is called an integral over the mass. 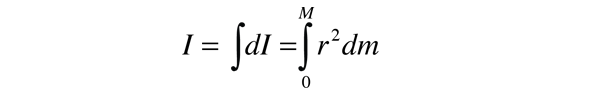 Usually, the mass element dm will be expressed in terms of the geometry of the object, so that the integration can be carried out over the object as a whole (for example, over a long uniform rod). Having called this a general form, it is probably appropriate to point out that it is a general form only for axes which may be called "principal axes", a term which includes all axes of symmetry of objects. The concept of moment of inertia for general objects about arbitrary axes is a much more complicated subject. The moment of inertia in such cases takes the form of a mathematical tensor quantity which requires nine components to completely define it.
|
Index Moment of inertia concepts | ||||
|
Go Back |