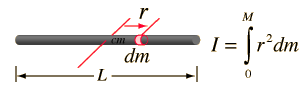
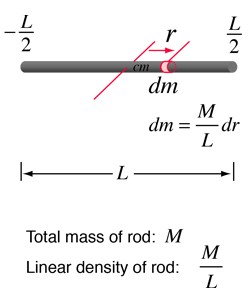
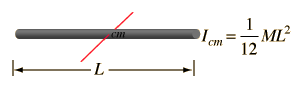
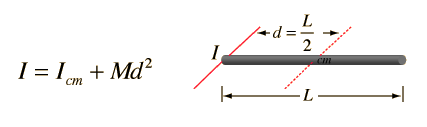
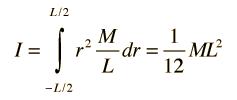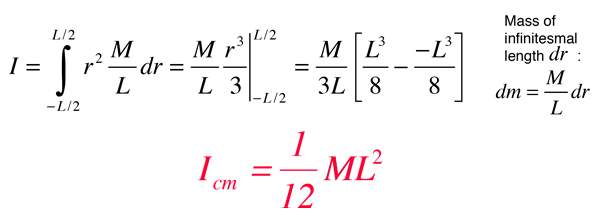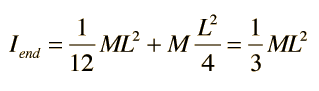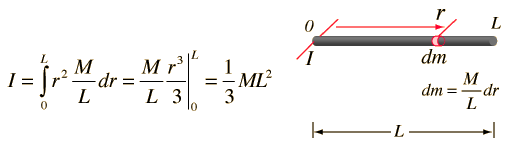Rotational and Linear Example
A mass m is placed on a rod of length r and negligible mass, and constrained to rotate about a fixed axis. If the mass is released from a horizontal orientation, it can be described either in terms of force and accleration with Newton's second law for linear motion, or as a pure rotation about the axis with Newton's second law for rotation. This provides a setting for comparing linear and rotational quantities for the same system. This process leads to the expression for the moment of inertia of a point mass.
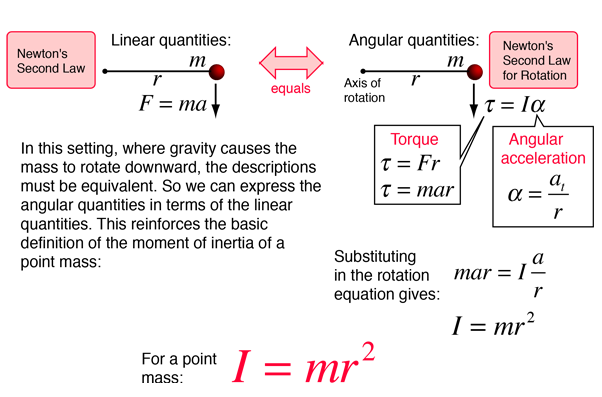
Moment of inertia concepts
Moment of inertia examples
| HyperPhysics***** Mechanics ***** Rotation | R Nave |