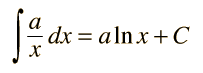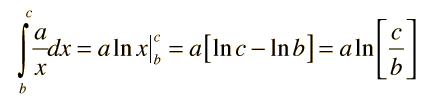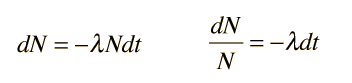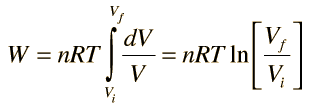Integrals of Polynomials
|
The integral of any polynomial is the sum of the integrals of its terms. A general term of a polynomial can be written 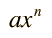 and the indefinite integral of that term is 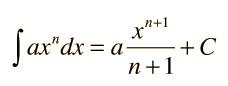 where a and C are constants. The expression applies for both positive and negative values of n except for the special case of n= -1. In the examples, C is set equal to zero. If definite limits are set for the integration, it is called a definite integral. |
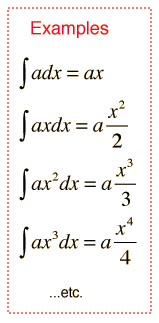 Case for n = -1 |
Applications
| HyperPhysics*****HyperMath*****Calculus | R Nave |