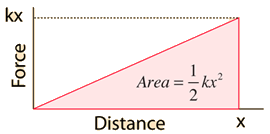
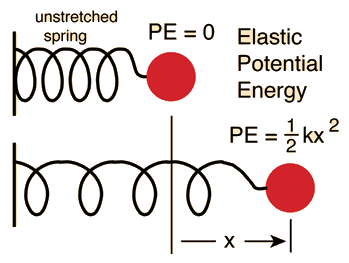
Elastic Potential Energy

Elastic potential energy is Potential energy stored as a result of deformation of an elastic object, such as the stretching of a spring. It is equal to the work done to stretch the spring, which depends upon the spring constant k as well as the distance stretched. According to Hooke's law, the force required to stretch the spring will be directly proportional to the amount of stretch.

Since the force has the form

F = -kx

then the work done to stretch the spring a distance x is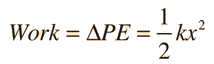


Show details

For spring constant k=N/m
and displacement x =m,
the potential energy = J.
You may enter data in any of the boxes. Then click on the active text for the quantity you wish to calculate. The values will not be forced to be compatible until you click on a quantity to calculate. 		Index

Energy concepts
 
HyperPhysics***** Mechanics R Nave
 Go Back





Spring Potential Energy

Since the change in Potential energy of an object between two positions is equal to the work that must be done to move the object from one point to the other, the calculation of potential energy is equivalent to calculating the work. Since the force required to stretch a spring changes with distance, the calculation of the work involves an integral.

The work can also be visualized as the area under the force curve:
Index

Energy concepts
 
HyperPhysics***** Mechanics R Nave
 Go Back