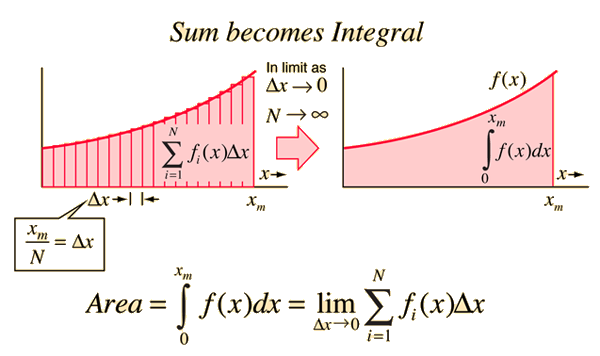
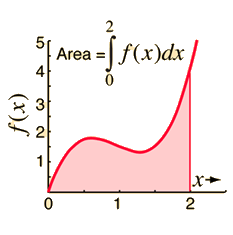
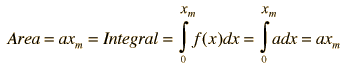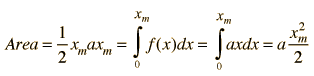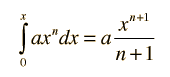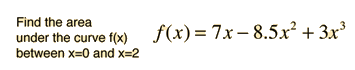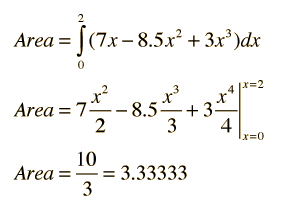Area Under a Curve
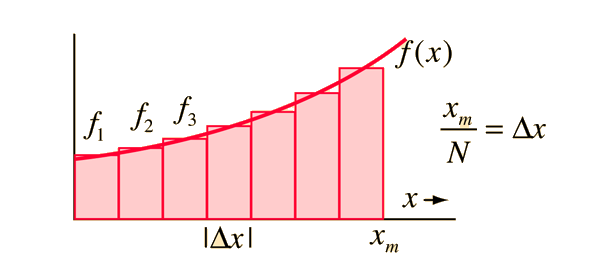
Formulating the area under a curve is the first step toward developing the concept of the integral. The area under the curve formed by plotting function f(x) as a function of x can be approximated by drawing rectangles of finite width and height f equal to the value of the function at the center of the interval.
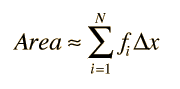
If the width of the rectangles is made smaller, then the number N is larger and the approximation of the area is better.
Show area integral for simple geometries.
Show area approximation of an integral.
| HyperPhysics*****HyperMath*****Calculus | R Nave |