Storing Energy in a Capacitor

The energy stored on a capacitor can be expressed in terms of the work done by the battery. Voltage represents energy per unit charge, so the work to move a charge element dq from the negative plate to the positive plate is equal to V dq, where V is the voltage on the capacitor. The voltage V is proportional to the amount of charge which is already on the capacitor.

Element of energy stored:

If Q is the amount of charge stored when the whole battery voltage appears across the capacitor, then the stored energy is obtained from the integral:

More detail Calculation

This energy expression can be put in three equivalent forms by just permutations based on the definition of capacitance C=Q/V.

Storing Energy in a Capacitor

When the switch is closed to connect the battery to the capacitor, there is zero voltage across the capacitor since it has no charge buildup. The voltage on the capacitor is proportional to the charge

Storing energy on the capacitor involves doing work to transport charge from one plate of the capacitor to the other against the electrical forces. As the charge builds up in the charging process, each successive element of charge dq requires more work to force it onto the positive plate. Summing these continuously changing quantities requires an integral.

Calculation More detail on integral

Note that the total energy stored QV/2 is exactly half of the energy QV which is supplied by the battery, independent of R!

Capacitor Energy Integral

Transporting differential charge dq to the plate of the capacitor requires work

But as the voltage rises toward the battery voltage in the process of storing energy, each successive dq requires more work. Summing all these amounts of work until the total charge is reached is an infinite sum, the type of task an integral is essential for. The form of the integral shown above is a polynomial integral and is a good example of the power of integration.

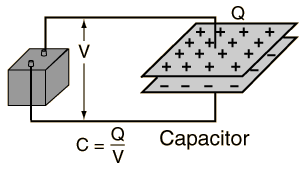
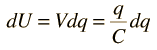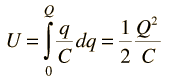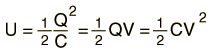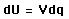Where did half of the capacitor charging energy go?

The problem of the "energy stored on a capacitor" is a classic one because it has some counterintuitive elements. To be sure, the battery puts out energy QV_b in the process of charging the capacitor to equilibrium at battery voltage V_b. But half of that energy is dissipated in heat in the resistance of the charging pathway, and only QV_b/2 is finally stored on the capacitor at equilibrium. The counter-intuitive part starts when you say "That's too much loss to tolerate. I'm just going to lower the resistance of the charging pathway so I will get more energy on the capacitor." This doesn't work, because the energy loss rate in the resistance I²R increases dramatically, even though you do charge the capacitor more rapidly. It's not at all intuitive in this exponential charging process that you will still lose half the energy into heat, so this classic problem becomes an excellent example of the value of calculus and the integral as an engineering tool.

Part of the intuitive part that goes into setting up the integral is that getting the first element of charge dq onto the capacitor plates takes much less work because most of the battery voltage is dropping across the resistance R and only a tiny energy dU = dqV is stored on the capacitor. Proceeding with the integral, which takes a quadratic form in q, gives a summed energy on the capacitor Q²/2C = CV_b²/2 = QV_b/2 where the V_b here is the battery voltage. So the bottom line is that you have to put out 2 joules from the battery to put 1 joule on the capacitor, the other joule having been irretrievably lost to heat - the 2nd Law of Thermodynamics bites you again, regardless of your charging rate. The non-intuitive nature of this problem is the reason that the integral approach is valuable.

Transporting differential charge dq to the plate of the capacitor requires work

Though it will not be shown here, if you proceed further with this problem by making the charging resistance so small that the initial charging current is extremely high, a sizable fraction of the charging energy is actually radiated away as electromagnetic energy. This crosses the threshold into antenna theory because not all the loss in charging was thermodynamic - but still the loss in the process was half the energy supplied by the battery in charging the capacitor.

So the energy supplied by the battery is E = CV_b², but only half that is on the capacitor - the other half has been lost to heat, or in the extremely low charging resistance case, to heat and electromagnetic energy.