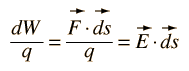Work and Voltage: Constant Electric Field
| The case of a constant electric field, as between charged parallel plate conductors, is a good example of the relationship between work and voltage. |
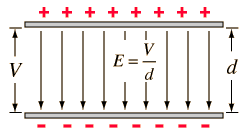 |
The electric field is by definition the force per unit charge, so that multiplying the field times the plate separation gives the work per unit charge, which is by definition the change in voltage.
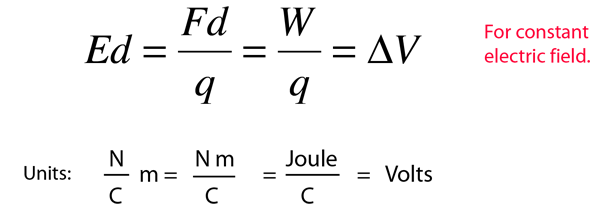
This association is the reminder of many often-used relationships:

| More general case |
Voltage concepts
Electric field concepts
| HyperPhysics***** Electricity and Magnetism | R Nave |