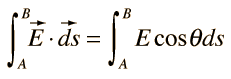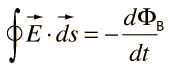Area Integral
 |
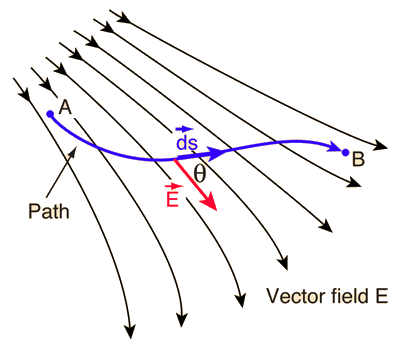
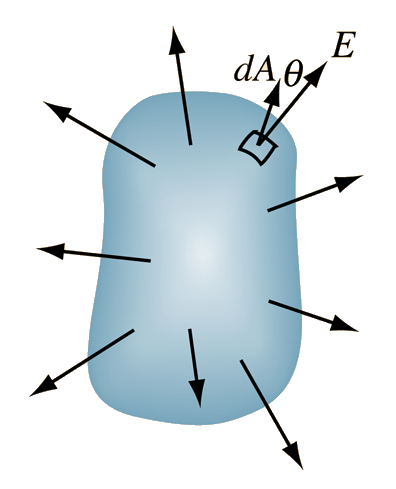
An area integral of a vector function E can be defined as the integral on a surface of the scalar product of E with area element dA. The direction of the area element is defined to be perpendicular to the area at that point on the surface. |
The outward directed surface integral over an entire closed surface is denoted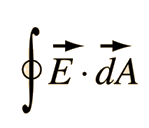 |
 |
| HyperPhysics*****HyperMath*****Calculus | R Nave |