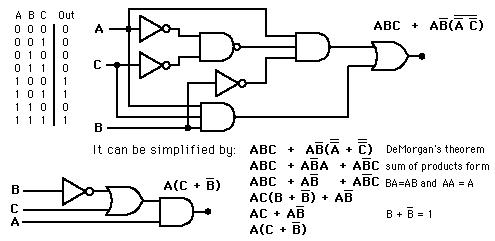
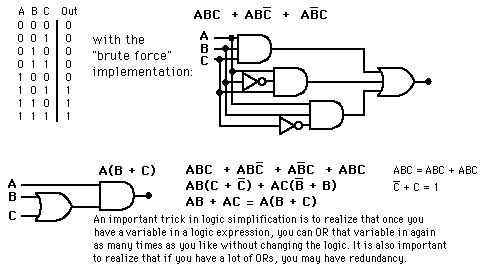
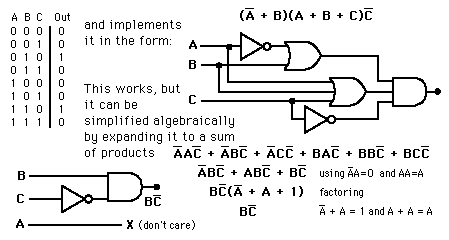
Algebraic Simplification of Logic Circuits
The logic form which comes from the direct application of the truth table will work, but it is often inefficient and takes an unneccessarily large number of gates. Logic expressions can often be simplified algebraicly, and although there is no fixed procedure, the following rules are often helpful.
- Use DeMorgan's theorem to put the original expression in a form involving only a sum of products.
- Check the form for common factors and use the single variable theorems to eliminate terms after factoring.
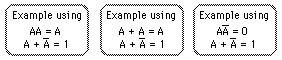
| Digital Logic Theorems | Digital Logic Functions |
Electronics concepts
Digital Circuits
| HyperPhysics*****Electricity and magnetism | R Nave |