Digital Logic
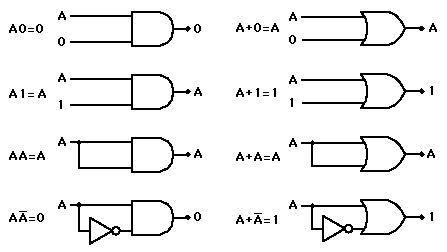
For two binary variables (taking values 0 and 1) there are 16 possible functions. The functions involve only three operations which make up Boolean algebra: AND, OR, and COMPLEMENT. They are symbolically represented as follows:
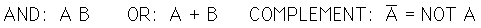
These operations are like ordinary algebraic operations in that they are commutative, associative, and distributive. There is a group of useful theorems of Boolean algebra which help in developing the logic for a given operation.
| Digital Logic Theorems | Digital Logic Functions |
Electronics concepts
Digital Circuits
| HyperPhysics*****Electricity and magnetism | R Nave |