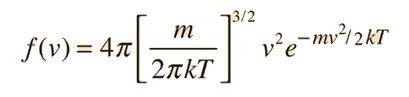Relation of particle velocity to height
Molecules which are higher in the atmosphere are there ultimately because they had a higher kinetic energy to convert into gravitational potential energy on some time scale. (Never mind the fact of untold billions of collisions on their way to that height!) On a very short time scale between collisions, some will rise incrementally higher than others from their starting points. It is that incremental height gain we consider here.)
If we have a population of particles which have energy sufficient to reach height z:

then a population with a little higher velocity can get a little higher

These energy considerations must account for the difference in population with height we observe in the barometric formula.
| Back to Discussion of Maxwell speed distribution development |
| Forward to Relate particle flux to the velocity distribution. |
Gas law concepts
Kinetic theory concepts
| HyperPhysics***** Heat and Thermodynamics | R Nave |