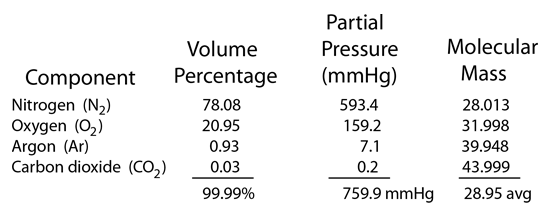
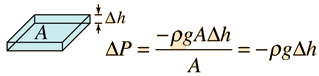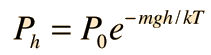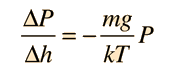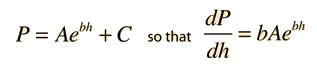The Barometric Formula
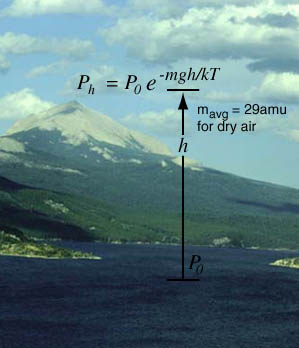 |
Note that the model calculation assumes a uniform temperature, and is therefore not a realistic model of the atmosphere. The temperature tends to decrease with height, so the model calculation will overestimate the pressure at a given height.
| Derivation of formula | Pressure at selected heights | Constituents of air |
Gas law concepts
Kinetic theory concepts
| HyperPhysics***** Thermodynamics | R Nave |