Fluid Pressure Measurement
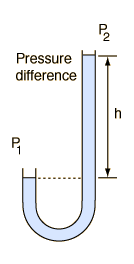
Since static fluid pressure is determined by the fluid density and depth, the depth or height difference of a given liquid is commonly used for pressure measurement:  | 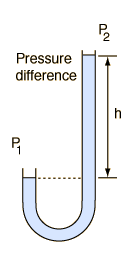 |
 |
The fact that the liquid levels are the same in these three manometers shows that the pressure in the glass manifold above them is uniform. This is under static conditions with no air flow through the system so that all parts of it are at atmospheric pressure. The fact that open liquids will seek a common level is the principle behind liquid levels for construction purposes. |
The flow in this system is from left to right, driven by a high pressure air supply. The system is said to have a positive gauge pressure exerted by the air supply. This pressure acts to push the manometer levels down, so the minimum height in the left manometer indicates that it is subjected to the highest pressure. |
 |
The fact that the center manometer has a higher level under these conditions of rapid air flow indicates that the pressure has been lowered in the constriction by the Bernoulli effect. Note that the liquid level in the right hand tube is slightly higher than the left tube, indicating that the pressure there is slightly less than that at the left hand tube. This is indicative of the normal pressure drop in a flowing fluid from Poiseuille's law since the diameters of the top tube are the same at the left and right tubes.
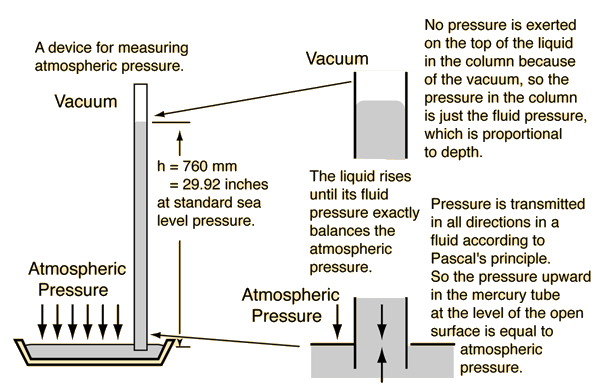
Pressure Calculation
Pressure concepts
| HyperPhysics***** Mechanics ***** Fluids | R Nave |