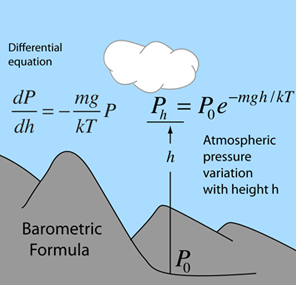
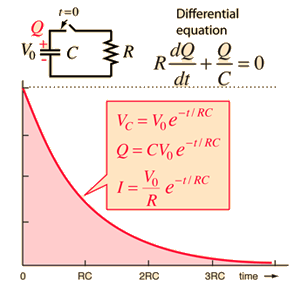
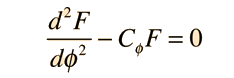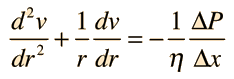Second Order Homogeneous DE

A linear second order homogeneous differential equation involves terms up to the second derivative of a function. For the case of constant multipliers, The equation is of the form

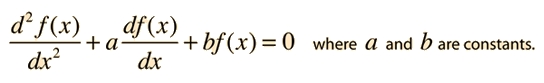
and can be solved by the substitution

The solution which fits a specific physical situation is obtained by substituting the solution into the equation and evaluating the various constants by forcing the solution to fit the physical boundary conditions of the problem at hand. Substituting gives

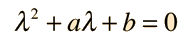
which leads to a variety of solutions, depending on the values of a and b. In physical problems, the boundary conditions determine the values of a and b, and the solution to the quadratic equation for λ reveals the nature of the solution.

Case I: Two real roots

For values of a and b such that

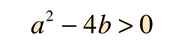
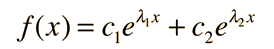
there are two real roots λ₁ and λ₂ which lead to a general solution of the form

Case II: A real double root

If a and b are such that

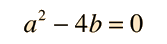
then there is a double root λ =-a/2 and the unique form of the general solution is

Case III: Complex conjugate roots

For values of a and b such that

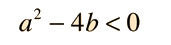
there are two complex conjugate roots of the form and the general solution is

The solution to the homogeneous equation is important on its own for many physical applications, and is also a part of the solution of the non-homogeneous equation.