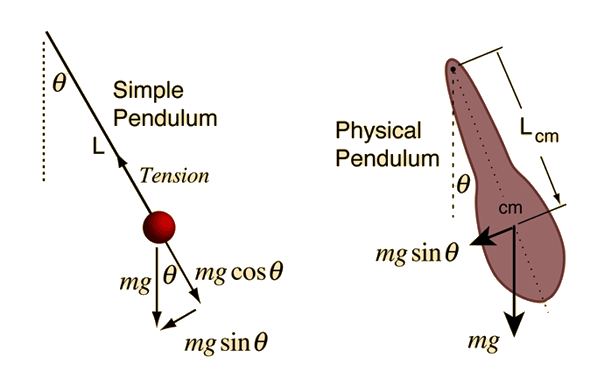
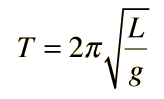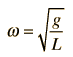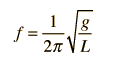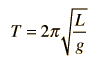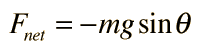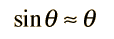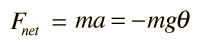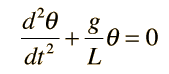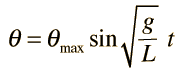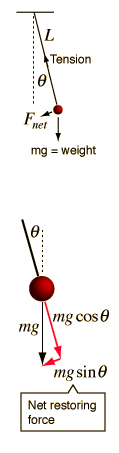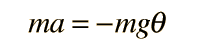Simple Pendulum

A simple pendulum is one which can be considered to be a point mass suspended from a string or rod of negligible mass. It is a resonant system with a single resonant frequency. For small amplitudes, the period of such a pendulum can be approximated by:

Show For pendulum length L = cm = m and acceleration of gravity g = m/s2 the pendulum period is T = s (Enter data for two of the variables and then click on the active text for the third variable to calculate it.) Note that the angular amplitude does not appear in the expression for the period. This expression for period is reasonably accurate for angles of a few degrees, but the treatment of the large amplitude pendulum is much more complex.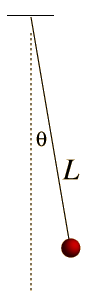

If the rod is not of negligible mass, then it must be treated as a physical pendulum.

Sean Carroll relates the story of Galileo's discovery of the fact that for small amplitudes, the period and frequency are unaffected by the amplitude. "In 1581, a young Galileo Galilei reportedly made a breakthrough discovery while he sat bored during a church service in Pisa. The chandelier overhead would swing gently back and forth, but it seemed to move more quickly when it was swinging widely (after a gust of wind, for example) and more slowly when it wasn't moving as far. Intrigued, Galileo decided to measure how much time it took for each swing, using the only approximately periodic event to which he had ready access: the beating of his own pulse. He found something interesting: The number of heartbeats between swings of the chandelier was roughly the same, regardless of whether the swings were wide or narrow. The size of the oscillations - how far the pendulum swung back and forth - didn't affect the frequency of those oscillations."

Pendulum Motion

The motion of a simple pendulum is like simple harmonic motion in that the equation for the angular displacement is

Show which is the same form as the motion of a mass on a spring: The anglular frequency of the motion is then given by compared to for a mass on a spring.

The frequency of the pendulum in Hz is given by

and the period of motion is then

Period of Simple Pendulum

A point mass hanging on a massless string is an idealized example of a simple pendulum. When displaced from its equilibrium point, the restoring force which brings it back to the center is given by:

Show For small angles θ, we can use the approximation Show in which case Newton's 2nd law takes the form Even in this approximate case, the solution of the equation uses calculus and differential equations. The differential equation is and for small angles θ the solution is:

Pendulum Geometry

The period of a simple pendulum for small amplitudes θ is dependent only on the pendulum length and gravity. For the physical pendulum with distributed mass, the distance from the point of support to the center of mass is the determining "length" and the period is affected by the distribution of mass as expressed in the moment of inertia I.

Pendulum Equation

The equation of motion for the simple pendulum for sufficiently small amplitude has the form

which when put in angular form becomes This differential equation is like that for the simple harmonic oscillator and has the solution: